如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点,则【 】
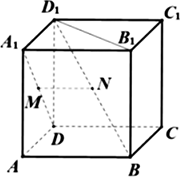
A、直线A1 D与直线D1 B垂直,直线MN//平面ABCD
B、直线A1 D与直线D1 B平行,直线MN//平面BDD1 B1
C、直线A1 D与直线D1 B相交,直线MN//平面ABCD
D、直线A1 D与直线D1 B异面,直线MN//平面BDD1 B1
如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点,则【 】

A、直线A1 D与直线D1 B垂直,直线MN//平面ABCD
B、直线A1 D与直线D1 B平行,直线MN//平面BDD1 B1
C、直线A1 D与直线D1 B相交,直线MN//平面ABCD
D、直线A1 D与直线D1 B异面,直线MN//平面BDD1 B1
A
圆台上、下底面积分别为π,4π侧面积为6π,这个圆台的体积是【 】
已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为【 】
如果棱台的两底面积分别是S,S',中截面的面积是S0,那么【 】
一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是【 】
如图,E,F分别为正方形的面ADD1A1、面BCC1B1的中心,则四边形在该正方形BFD1E的面上的射影可能是________.(要求:把可能的图的序号都填上)
若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的侧面积是________.
若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积是【 】
已知圆柱的底面圆半径为1,高为2,AB为上底面圆的一第直径,C是下底面圆周上的一个动点,则ABC的面积取值范围为__________.
已知圆锥的侧面积 (单位: cm2) 为 2π, 且它的侧面展开图是一个半圆, 则这个圆锥的底面半径 (单位: cm) 为_______.
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则【 】