母线长为1的圆锥体积最大时,其侧面展开图圆心用ϕ等于【 】
A、2 /3 π
/3 π
B、2 /3 π
/3 π
C、 π
π
D、(2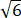 )/3 π
)/3 π
设双曲线x2/a2 - y2/b2 =1(0<a<b)的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为/4 c,则双曲线的离心率为【 】
等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为【 】
椭圆的极坐标方程为ρ=3/(2-cosθ ),则它在短轴上的两个顶点的极坐标是【 】
等比数列{an}的首项a1=-1,前n项和为Sn,若S10/S5 =31/32,则Sn 等于【 】
将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,,则三棱锥D-ABC的体积为【 】
若0<α<π/2,则acrsin[cos(π/2+a) ]+arccos[sin(π+α) ]等于【 】
当-π/2≤x≤π/2时,函数f(x)=sinx+ cosx 【 】
已知圆锥的中截面周长为a,母线长为l,则它的侧面积等于______.
在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为120°。若要光源恰好照亮整个广场,则其高度应为________(精确到0.1m)。
设圆锥底面圆周上两点A,B间的距离为2,圆锥顶点到直线AB的距离为,AB和圆锥的轴的距离为1,则该圆锥的体积为________.
如图,四边形ABCD为正方形, ED⊥平面ABCD,FB//ED,AB=ED=2FB,记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则【 】
已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,AP=2,点C在底面圆周上,且二面角P-AC-O为45°,则【 】
已知直四棱柱 ABCD − A1B1C1D1 的棱长均为 2, ∠BAD = 60◦. 以 D1 为球心, 为半径的球面与侧面 BCC1B1 的交线长为__________.
某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为【 】
若棱长为 2 的正方体的顶点都在同一球面上, 则该球的表面积为【 】
某几何体的三视图 (单位: cm) 如图所示, 则该几何体的体积 (单位: cm3) 是【 】
已知正方形的边长为 a ,求侧面积等于这个正方形的面积、高等于这个正方形边长的直圆柱体的体积
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
如下图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB, 将剩余部分沿OC,OD折叠,使OA,OB重合,则A(B),C,DCO为顶点的四面体的体积是_______.