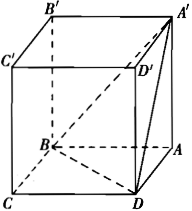
如果正方体ABCD-A′B′C′D′的棱长为a，则A′-ABD的体积是【 】
A、a3/2
B、a3/3
C、a3/4
D、a3/6
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
如图，已知圆心为O、半径为1的圆与直线l相切于点A，一动点P自切点A沿直线l向右移动时，取弧的长为2/3AP，直线PC与直线AO交于点M.又知当AP=3π/4时，点P的速度为v，求这时点M的速度.
在△ABC中，∠A,∠B,∠C所对的边分别为a,b,c,且c=10, cosA/cosB=b/a=4/3, P为△ABC的内切圆上的动点.求点P到顶点A,B,C的距离的平方和的最大值与最小值.
求经过定点M(1,2),以y轴为准线,离心率为1/2的椭圆的左顶点的轨迹方程.
设p≠0，实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.
设c,d,x为实数，c≠0,x为未知数.讨论方程 = -1在什么情况下有解.有解时求出它的解.
已知三个平面两两相交，有三条交线.求证这三条交线交于一点或互相平行.
画出极坐标方程(ρ-2)(θ-π/4)=0(ρ>0)的曲线.
要排一张有6个歌唱节目和4个舞蹈节目的演出节目单，任何两个舞蹈节目不得相信，问：有多少种不同的排法？（只要写出式子，不必计算）
已知圆锥体的底面半径为R，高为H.求内接于这个圆锥体并且体积最大的圆柱体的高h(如图).
如图，E,F分别为正方形的面ADD1A1、面BCC1B1的中心，则四边形在该正方形BFD1E的面上的射影可能是________.(要求：把可能的图的序号都填上)
如图,在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=1/2. (I)求四棱锥S-ABCD的体积;(Ⅱ)求面SCD与面SBA所成二面角的正切值.
已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为【 】
在一个正方体中，过顶点A的三条棱的中点分别为E，F，G，该正方体截去三棱锥A-EFG后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是【 】
已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为________.
以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某三棱锥的三视图，则所选侧视图和俯视图的编号依次为______ ( 写出符合要求的一组答案即可).
如图，四棱锥P-ABCD的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PB⊥AM．(1) 证明：平面PAM⊥平面 PBD；(2) 若PD=DC=1，求四棱锥P-ABCD 的体积.
如图，长方体ABCD-A1 B1 C1 D1中，已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点，求三棱锥C-PAD的体积；(2)求直线AB1与平面ACC1 A1的夹角大小.
在正方体ABCD-A1B1C1D1中，E，F分别为AB,BC的中点，则【 】
如图,从一个棱长为6米的正方体中裁去两个相同的正三棱锥，若正三棱锥的边长AB为4√2,则剩余何体的表面积为【 】
下列物体中，能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点，则【 】
如图，已知长方体的对角线长为l，它与底面所成的角为α，底面两条对角线的夹角为β.求长方体的积体.
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线，垂足为E，证明A1E:EC=1:2.