如图,E,F分别为正方形的面ADD1A1、面BCC1B1的中心,则四边形在该正方形BFD1E的面上的射影可能是________.(要求:把可能的图的序号都填上)
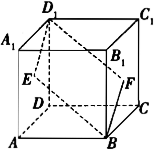

如图,E,F分别为正方形的面ADD1A1、面BCC1B1的中心,则四边形在该正方形BFD1E的面上的射影可能是________.(要求:把可能的图的序号都填上)


②③
已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是【 】
如果轴截面为正方形的圆柱的侧面积是S,那么圆柱的体积等于【 】
在球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a.那么这个球面的面积是________.
体积相等的正方体、球、等边圆柱(即底面直径与母线 相等的圆柱)的全面积分别为S1,S2,S3,那么它们的 大小关系为【 】
已知过球面上A,B,C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积是【 】
正方体的全面积是a2,它的顶点都在球面上,这个球的表面积是【 】
已知圆台上、下底面圆周都在球面上,且下底面过球心,母线与底面所成的角为π/3,则圆台的体积与球的体积之比为__________.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.(1)求证:AF⊥DB;2)如果圆柱与三棱锥D-ABE的体积比等于3πr,求直线DE与平面ABCD所成的角.
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则【 】
某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为【 】
某几何体的三视图 (单位: cm) 如图所示, 则该几何体的体积 (单位: cm3) 是【 】
如图是一个多面体的三视图, 这个多面体某条棱的一个端点在正视图中对应的点为 M, 在俯视图中对应的 点为 N, 则该端点在侧视图中对应的点为【 】
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是【 】
如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为【 】
以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为______ ( 写出符合要求的一组答案即可).
在一个正方体中,过顶点A的三条棱的中点分别为E,F,G,该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如右图所示,则相应的侧视图是【 】