如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
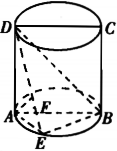
(1)求证:AF⊥DB;
2)如果圆柱与三棱锥D-ABE的体积比等于3πr,求直线DE与平面ABCD所成的角.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.

(1)求证:AF⊥DB;
2)如果圆柱与三棱锥D-ABE的体积比等于3πr,求直线DE与平面ABCD所成的角.
(1)根据圆柱性质,DA⊥平面ABE.∵EB⊂平面ABE,∴DA⊥EB.∵AB是圆柱底面的直径,点E在圆周上,∴AE⊥BB又 AE∩AD=A,故得EB⊥平面DAE.AF⊂平面DAE,∴EB⊥AF.又AF⊥DE,且EB∩DE=E,故得AF⊥平面DEB∵DB⊂平面DEB,∴AF⊥DB.(2)过点E作EH⊥AB,H是垂足,连接DH. 根据圆柱性质,平面ABCD⊥平面ABE,AB是交线且EH⊂平面...
查看完整答案已知正方形的边长为 a ,求侧面积等于这个正方形的面积、高等于这个正方形边长的直圆柱体的体积
如果轴截面为正方形的圆柱的侧面积是S,那么圆柱的体积等于【 】
已知圆柱的轴截面是正方形,它的面积是4cm2,那么这个圆柱的体积是__________cm3 (结果中保留π).
已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是【 】
一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是【 】
已知圆柱的底面圆半径为1,高为2,AB为上底面圆的一第直径,C是下底面圆周上的一个动点,则ABC的面积取值范围为__________.
已知直四棱柱 ABCD − A1B1C1D1 的棱长均为 2, ∠BAD = 60◦. 以 D1 为球心, 为半径的球面与侧面 BCC1B1 的交线长为__________.
某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为【 】
若棱长为 2 的正方体的顶点都在同一球面上, 则该球的表面积为【 】
某几何体的三视图 (单位: cm) 如图所示, 则该几何体的体积 (单位: cm3) 是【 】
已知圆锥的侧面积 (单位: cm2) 为 2π, 且它的侧面展开图是一个半圆, 则这个圆锥的底面半径 (单位: cm) 为_______.
已知圆锥体的底面半径为R,高为H.求内接于这个圆锥体并且体积最大的圆柱体的高h(如图).
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
如下图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB, 将剩余部分沿OC,OD折叠,使OA,OB重合,则A(B),C,DCO为顶点的四面体的体积是_______.
如图,已知正三棱柱ABC-A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F-BC-A的平面角为γ,则【 】
过一定点作一直线 AB 平行于一定平面 P,且与另一定平面 Q 所成之角等于定角 θ.
在120°的二面角P-α-Q的两个面P和Q内,分别有点A和B . 已知点A和点B到棱α的距离分别为2和4,且线段AB=10.(1) 求直线AB和棱α所成的角;(2) 求直线AB和平面Q所成的角.
已知空间四边形ABCD中AB=BC,CD=DA,M,N,P,Q分别是边AB,BC,CD,DA的中点(如图).求证MNPQ是一个矩形.