如图, 三棱台 ABC − DEF 中, 平面 ACFD ⊥ 平面 ABC, ∠ACB = ∠ACD = 45°, DC = 2BC.
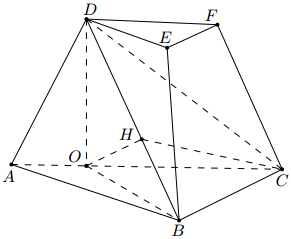
(I) 证明: EF ⊥ DB;
(II) 求 DF 与面 DBC 所成角的正弦值.
如图, 三棱台 ABC − DEF 中, 平面 ACFD ⊥ 平面 ABC, ∠ACB = ∠ACD = 45°, DC = 2BC.

(I) 证明: EF ⊥ DB;
(II) 求 DF 与面 DBC 所成角的正弦值.
(I) 如图, 过点 D 作 DO ⊥ AC , 交直线 AC 于点 O, 连结 OB. 由 ∠ACD = 45º, DO ⊥ AC 得 CD = CO.由平面 ACFD ⊥ 平面 ABC 得 DO ⊥ 平面 ABC, 所以 DO ⊥ BC.由 ∠ACB = 45º, BC=1/2 CD=/2 CO 得 BO ⊥ BC. 所以 BC ⊥ 平面 BDO, 故 BC ⊥ DB.由三棱台 ABC − DEF 得 BC // EF , 所以 EF ⊥ DB.(II)过点 O 作 OH ⊥ BD, 交直线 B...
查看完整答案在锐角 △ABC 中, 角 A, B, C 的对边分别为 a, b, c, 且 2bsinA − a = 0.(I) 求角 B;(II) 求 cosA + cosB + cosC 的取值范围.
已知单位向量 e1, e2 满足|e1-e2 |≤, 设 a = e1 + e2, b = 3e1 + e2, 向量 a, b 的夹角为 θ, 则 cos2θ的最小值为_______.
已知直线 y = kx + b (k > 0) 与圆 x2 + y2 = 1 和圆 (x − 4)2 + y2 = 1 均相切, 则 k = _______, b = _______.
已知圆锥的侧面积 (单位: cm2) 为 2π, 且它的侧面展开图是一个半圆, 则这个圆锥的底面半径 (单位: cm) 为_______.
已知 tanθ = 2, 则 cos2θ = _______, tan(θ − π/4) = _______.
二项展开式 (1 + 2x)5 = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5, 则 a4 = _______, a1 + a3 + a5 = _______.
我国古代数学家杨辉、宋世杰等研究过高阶等差数列求和问题, 如数列 {n(n+1)/2} 就是二阶等差数列,数列{n(n+1)/2} (n ∈ N∗) 的前 3 项和是________.
已知 a, b ∈ R 且 ab ≠ 0, 若 (x − a)(x − b)(x − 2a − b) ⩾ 0 在 x ⩾ 0 上恒成立, 则【 】
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.
在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为【 】
如图,已知正三棱柱ABC-A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F-BC-A的平面角为γ,则【 】
下列五个正方体图形中,l是正方体的一条对角线,点 M,N,P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是________(写出所有符合要求的图形序号).
已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体,其中两个面分别位于平面P1和P2上,下面哪条直线可能是该四面体的一条棱【 】
Find the equation of the projection of the linex=z+2,y=2z-4 upon the plane x+y- z = 0.
自一平面外之一点 A向平面上作 AB 垂线,CD 为平面内之任一线,AE线垂直于CD,证BE线垂直于CD.
过一定点作一直线 AB 平行于一定平面 P,且与另一定平面 Q 所成之角等于定角 θ.
已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知:两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F,设A1E=m,AF=n. 求证:EF=.