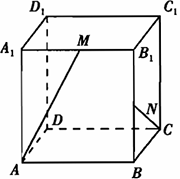
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
A、 /2
/2
B、 /10
/10
C、3/5
D、2/5
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】

A、 /2
/2
B、 /10
/10
C、3/5
D、2/5
D
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点,则【 】
如图,已知长方体的对角线长为l,它与底面所成的角为α,底面两条对角线的夹角为β.求长方体的积体.