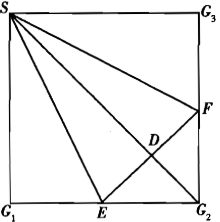
在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF中点. 现沿SE、SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G.那么,在四面体S-EFG中必有【 】
A、SG⊥△EFG所在平面
B、SD⊥△EFG所在平面
C、GF⊥△SEF所在平面
D、GD⊥△SEF所在平面
在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF中点. 现沿SE、SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G.那么,在四面体S-EFG中必有【 】

A、SG⊥△EFG所在平面
B、SD⊥△EFG所在平面
C、GF⊥△SEF所在平面
D、GD⊥△SEF所在平面
A
如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.
如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明:BC⊥AD;(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.
已知空间四边形ABCD中AB=BC,CD=DA,M,N,P,Q分别是边AB,BC,CD,DA的中点(如图).求证MNPQ是一个矩形.
如图,在三棱锥S-ABC中,S在底面上的射影N位于底面的高CD上;M是侧棱SC上的一点,使截面MAB与底面所成的角等于∠NSC,求证:SC垂直于截面MAB.
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.
如图,已知正三棱柱ABC-A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F-BC-A的平面角为γ,则【 】
下列五个正方体图形中,l是正方体的一条对角线,点 M,N,P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是________(写出所有符合要求的图形序号).
已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体,其中两个面分别位于平面P1和P2上,下面哪条直线可能是该四面体的一条棱【 】
Find the equation of the projection of the linex=z+2,y=2z-4 upon the plane x+y- z = 0.