如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.
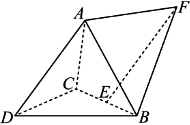
(1)证明:BC⊥AD;
(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.
如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.

(1)证明:BC⊥AD;
(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.
(1)连接AE,DE,因为E为BC的中点,且DB=DC,∴DE⊥BC①,∵DA=DB=DC,∠ADB=∠ADC=60°,∴△ACD与△ABD均为等边三角形,∴AC=AB,从而AE⊥BC②,由①②,AE∩DE=E,AE,DE⊂平面ADE,∴BC⊥平面ADE,∵AD⊂平面ADE,∴BC⊥AD.(2)不妨设DA=DB=DC=2,∵BD⊥CD,∴BC=2√2,DE=AE=√2.∴AE²+DE²=AD²=4,∴AE⊥DE,又∵AE⊥BC,DE∩BC=E,DE,BC⊂平面BCD,∴AE⊥平面BCD.以点E为原点,ED,EB,EA所在直线分别为x,y,z轴,建立空间直角坐标系,则A(0,0,√2),B(0,√2,0)...
查看完整答案如图,四棱锥P-ABCD 的底面是矩形,PD⊥底面ABCD,PD = DC = 1,M 为 BC 的中点,且 PB⊥AM.(1) 求 BC;(2) 求二面角A-PM-B的正弦值.
执行如图的程序框图, 若输入 k = 0, a = 0, 则输出的 k 为【 】
正三棱台高为1,上下底边长分别为3√3和4√3,所有顶点在同一球面上,则球的表面积是【 】
如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E是PB的中点.(1)求证:OE//平面PAC;(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样方法作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,则不同的抽样结果共有【 】种.
已知α为锐角,cosα=(1+√5)/4,则sin(α/2)=【 】
已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,AP=2,点C在底面圆周上,且二面角P-AC-O为45°,则【 】