高中数学-高考试题(全国甲·理 2021年空间平面及关系)

单项选择（2021年全国甲·理）

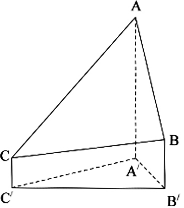
2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m)，三角高程测量法是珠穆高峰测量法之一，下图是三角高程测量法的一个示意图，现有A，B，C三点，且A,B,C在同水平面上的投影A',B',C'满足∠A' C' B'=45°,∠A' B'C'=60°，由C点测得B点的仰角为15°,BB'与CC'的差为100，由B点测得A点的仰角为45°，则A,C两点到水平面A'B'C'的高度差AA'-CC'约为(≈1.732)【】

A、346

B、373

C、446

D、473

答案解析

B

讨论

高中数学

等比数列{an}的公比为q，前n项和为Sn，设甲：q>0，乙：{Sn}是递增数列，则【】

在一个正方体中，过顶点A的三条棱的中点分别为E，F，G，该正方体截去三棱锥A-EFG后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是【】

已知F1,F2是双曲线C的两个焦点，P为C上一点，且∠F1PF2=60°,|PF1|=3|PF2|，则C的离心率为【】

青少年视力是社会普遍关注的问题，视力情况可借助视力表测量，通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录法的数据V满足L=5+lgV，已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为(≈1.259)【】

已知(1-i)2z=3+2i，则z=【】

为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图，下面结论中不正确的是【】

设集合M={x│0<x<4},N={x|1/3≤x≤5}，则M∩N=【】

已知函数f(x)=x(1-lnx).(1)讨论f(x)的单调性；(2)设a,b为两个不相等的正数，且blna-alnb=a-b，证明：2<1/a+1/b<e.

在平面直角坐标系xOy中，已知点F1(-,0),F2 (,0)，点M满足：|MF1|-|MF2|=2.记M的轨迹为C.(1)求C的方程；(2)设点T在直线x=1/2上，过T的两条直线分别交C于A,B两点和P,Q两点，且|TA|∙|TB|=|TP|∙|TQ|，求直线AB的斜率与直线PQ的斜率之和.

如图，在三棱锥A-BCD中，平面ABD丄平面BCD，AB=AD,O为BD的中点. (1)证明：OA⊥CD；(2)若△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，且二面角E-BC-D的大小为45°，求三棱锥A-BCD的体积.

空间解析几何

如图所示，为了制作一个圆柱形灯笼，先要制作4 个全等的矩形骨架，总计耗用9.6 米铁丝。骨架将到柱底面8 等分，再用S 平方米塑輯片制成圆柱的侧面和下底面（不安装上底面).（Ⅰ）当圆柱底面半径r 为何值时， S 取得最大值？并求出该最大值（结果精确到0.01 平方米）；（Ⅱ）在灯笼内，以矩形骨架的頂点为端点，安装一些霓虹灯，当灯笼底面半径为0.3 米时，求图中两根直线型霓虹灯A1B3,A3B5所在异面直线所成角的大小（结果用反三角函数值表示).

在xOy平面上，四边形ABCD的四个顶点坐标依次为(0,0),(1,0),(2,1)及(0,3).求这个四边形绕x轴旋转一周所得到的几何体的体积.

如图，OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为【】

如图所示四面体A-BCD中，AB,BC,BD两两互相垂直，且AB=BC=2，E是AC的中点，异面直线AD与BE所成的角大小为arccos /10，求四面体A-BCD的体积.

如图，在正四棱柱ABCD-A1 B1 C1 D1中，AB=2,AA1=4，点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.(1)证明：B2 C2//A2 D2;(2)点P在棱BB1上，当二面角P-A2 C2-D2为150°时，求B2 P.

如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径, AE = AD. △ABC 是底面的内接正三角形,P 为 DO 上一点, PO = DO.(1) 证明: PA ⊥ 平面 PBC;(2) 求二面角 B − PC − E 的余弦值.

如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;(2) 设 O 为 △A1B1C1 的中心, 若 AO = AB = 6, AO//平面 EB1C1F , 且 ∠MPN = π/3 , 求四棱锥 B −EB1C1F 的体积.

如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.(1) 证明: 当 AB = BC 时, EF ⊥ AC;(2) 证明: 点 C1 在平面 AEF 内.

如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.(1) 证明: 点 C1 在平面 AEF 内;(2) 若 AB = 2, AD = 1, AA1 = 3, 求二面角 A − EF − A1 的正弦值.

如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.

空间平面及关系

如图, 在三棱柱 ABC − A1B1C1 中, CC1⊥平面 ABC, AC ⊥ BC, AC = BC = 2, CC1 = 3, 点 D, E 分别在棱 AA1 和棱 CC1 上, 且 AD = 1, CE = 2, M 为棱 A1B1 的中点.(I) 求证: C1M ⊥ B1D;(II) 求二面角 B − B1E − D 的正弦值;(III) 求直线 AB 与平面 DB1E 所成角的正弦值.

如图，三棱锥A-BCD中，DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明：BC⊥AD;(2)点F满足(EF)→=(DA)→，求二面角D-AB-F的正弦值.

在三棱柱 ABC − A1B1C1 中, AB ⊥ AC, B1C ⊥ 平面 ABC, E, F 分别是 AC, B1C 的中点.(1) 求证: EF // 平面 AB1C1;(2) 求证: 平面 AB1C ⊥ 平面 ABB1.

直升飞机上一点 P 在地平面 M 上的正射影是 A ．从P看地平面上一物体 B （不同于 A ) ，直线P B 垂直于飞机窗玻璃所在的平面 N（如图）．证明：平面 N 必与平面 M 相交，且交线 l 垂直于 AB.

如图，在三棱锥S-ABC中，S在底面上的射影N位于底面的高CD上；M是侧棱SC上的一点，使截面MAB与底面所成的角等于∠NSC，求证：SC垂直于截面MAB.

如图，设平面AC和BD相交于BC，它们所成的一个二面角为45°，P为面AC内的一点，Q为面BD内的一点.已知直线MQ是直线PQ在平面BD内的射影，并且M在BC上，又设PQ与平面BD所成的角为β，∠CMQ=θ(0°<θ<90°)，线段PM的长为a.求线段PQ的长.

如图，已知二面角α-AB-β的平面角是锐角，C是平面α内的一点（它不在棱AB上），点D是点C在平面β上的射影，点E是棱AB上满足∠CEB为锐角的任意一点，那么【】.

如图，四棱锥S-ABCD的底面是边长为1的正方形，侧棱SB垂直于底面，并且SB=，用α表示∠ASD，求sinα的值.

如图，在三棱锥S-ABC中，SA⊥底面ABC,AB⊥BC.DE垂直平分SC，且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.

如图，平面α,β相交于直线MN，点A在平面α上，点B在平面β上，点C在直线MN上，∠ACM=∠BCN=45°，A-MN-B是60°的二面角，AC=1. 求：(1) 点A到平面β的距离；(2) 二面角A-BC-M的大小（用反三角函数表示）.