高中数学-高考试题(江苏省 2020年空间平面及关系)

证明题（2020年江苏省）

在三棱柱 ABC − A₁B₁C₁ 中, AB ⊥ AC, B₁C ⊥ 平面 ABC, E, F 分别是 AC, B₁C 的中点.

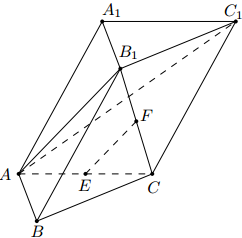
(1) 求证: EF // 平面 AB₁C₁;

(2) 求证: 平面 AB₁C ⊥ 平面 ABB₁.

答案解析

(1) 因为 E, F 分别是 AC, B1C 的中点, 所以 EF // AB1.又 EF ̸⊂ 平面 AB1C1, AB1 ⊂ 平面 AB1C1, 所以 EF // 平面 AB1C1.(2) 因为 B1C ⊥ 平面 ABC, AB ⊂ 平面 ...

查看完整答案

讨论

高中数学

在平面直角坐标系 xOy 中, 已知 P(/2,0), A、 B 是圆 C : x2+(y-1/2)2=36上的两个动点, 满足 P A = P B, 则 △P AB 面积的最大值是______.

在 △ABC 中, AB = 4, AC = 3, ∠BAC = 90º, D 在边 BC 上, 延长 AD 到 P , 使得 AP = 9. 若=m+(3/2-m) (m 为常数), 则 CD 的长度是__________.

已知 5x2y2 + y4 = 1 (x, y ∈ R), 则 x2 + y2 的最小值是________.

设 {an} 是公差为 d 的等差数列, {bn} 是公比为 q 的等比数列. 已知 {an + bn} 的前 n 项和为 Sn = n2 − n + 2n − 1 (n ∈ N∗), 则 d + q 的值是______.

将函数y=3sin⁡(2x+π/4)的图象向右平移 π/6 个单位长度, 则平移后的图像中与 y 轴最近的对称轴的方程是__________.

如图, 六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的. 已知螺帽的底面正六边形边长为 2cm, 高为 2cm, 内孔半径为 0.5cm, 则此六角螺帽毛坯的体积是 __________cm3.

已知sin2(π/4+α)=2/3, 则sin2α的值是_______.

已知 y = f(x) 是奇函数, 当 x ⩾ 0 时, f(x) = x2/3 , 则 f(−8) 的值是______.

在平面直角坐标系 xOy 中, 若双曲线 x2/a2 -y2/5=1 (a > 0) 的一条渐近线方程为 y=/2 x , 则该双曲线的离心率是_______.

如图是一个算法流程图, 若输出 y 的值为 −2, 则输入 x 的值是______.

空间解析几何

Find the equation of the plane passing through the line (x-x1)/a1 =(y-y1)/b1 =(z-z1)/c1 which is parallel to the (x-x2)/a2 =(y-y2)/b2 =(z-z2)/c2 .

Find the equation of the sphere which passes through (1,5,-3),(-3,0,0) which center on the 3x+y+z=0,x+2y +1 = 0.

自一平面外之一点 A向平面上作 AB 垂线，CD 为平面内之任一线，AE线垂直于CD，证BE线垂直于CD.

过一定点作一直线 AB 平行于一定平面 P，且与另一定平面 Q 所成之角等于定角 θ.

如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;(2) 设 O 为 A1B1C1 的中心, 若 AO // 面 EB1C1F , 且 AO = AB, 求直线 B1E 与平面 A1AMN 所成角的正弦值.

日晷是中国古代用来测定时间的仪器, 利用与晷面垂直的晷针投射到晷面的影子来测定时间. 把地球看成一个球 (球心记为 O) , 地球上一点 A 的纬度是指 OA 与地球赤道所在平面所成角, 点 A 处的水平面是指过点 A 且与 OA 垂直的平面. 在点 A 处放置一个日晷, 若晷面与赤道所在平面平行, 点 A 处的纬度为北纬 40°, 则晷针与点 A 处的水平面所成角为【】

已知 ABCD 是边长为 1 的正方形, 绕其中一条轴 AB 旋转成一个圆柱.(1) 求该圆柱的表面积;(2) 将 DC 旋转 90° 至 C1D1, 求线 C1D 与平面 ABCD 的夹角.

如图, 三棱台 ABC − DEF 中, 平面 ACFD ⊥ 平面 ABC, ∠ACB = ∠ACD = 45°, DC = 2BC.(I) 证明: EF ⊥ DB;(II) 求 DF 与面 DBC 所成角的正弦值.

如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.

如图，OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为【】

空间平面及关系

如图，已知ABCD和CDEF都是直角梯形，AB//DC，DC//EF，AB=5，DC=3，EF=1，∠BAD=∠CDE=60°，二面角F-DC-B的平面角为60°．设M，N分别为AE,BC的中点．（1）证明：FN⊥AD；（2）求直线BM与平面ADE所成角的正弦值．

如图,在直三棱柱ABC-A1B1C1中，底面是等腰直角三角形，∠ACB=90°.侧棱AA1=2，D,E分别是CC1与A1B的中点，点E在平面ABD上的射影是△ABD的重心G.(I)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);(Ⅱ)求点A1到平面AED的距离.

直三棱柱ABC-A1B1C1中，AA1=AB=AC=2,AA1⊥AB,D为A1B1的中点，E为AA1的中点，F为CD的中点.(1)求证：EF//ABC平面；(2)求直线BE与平面CC1D夹角的正弦值；(3)求平面A1CD与平面CC1D夹角的余弦值.

如图，在正四棱柱ABCD-A1 B1 C1 D1中，AB=2,AA1=4，点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.(1)证明：B2 C2//A2 D2;(2)点P在棱BB1上，当二面角P-A2 C2-D2为150°时，求B2 P.

坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素，安装灯带可以勾勒出建筑轮廓，展现造型之美.如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形，若AB=25m,BC=AD=10m，且等腰梯形所在的平面、等腰三角形所在的平面与平面ABCD的夹角的正切值均为√14/5，则该五面体的所有棱长之和为【】

如图，在三棱锥P-ABC中，PA⊥平面ABC,PA=AB=BC=1,PC=√3. (1)求证：BC⊥平面PAB；(2)求二面角A-PC-B的大小.

如图，四棱锥P-ABCD中，PA⊥底面ABCD,PA=AC=2,BC=1,AB=√3. (Ⅰ)若AD⊥PB，证明：AD//平面PBC；(Ⅱ)若AD⊥DC，且二面角A-CP-D的正弦值为√42/7，求AD.

如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径, AE = AD. △ABC 是底面的内接正三角形,P 为 DO 上一点, PO = DO.(1) 证明: PA ⊥ 平面 PBC;(2) 求二面角 B − PC − E 的余弦值.

如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;(2) 设 O 为 △A1B1C1 的中心, 若 AO = AB = 6, AO//平面 EB1C1F , 且 ∠MPN = π/3 , 求四棱锥 B −EB1C1F 的体积.

如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.(1) 证明: 当 AB = BC 时, EF ⊥ AC;(2) 证明: 点 C1 在平面 AEF 内.