直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,AA1⊥AB,D为A1B1的中点,E为AA1的中点,F为CD的中点.
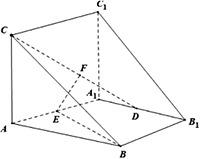
(1)求证:EF//ABC平面;
(2)求直线BE与平面CC1D夹角的正弦值;
(3)求平面A1CD与平面CC1D夹角的余弦值.
直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,AA1⊥AB,D为A1B1的中点,E为AA1的中点,F为CD的中点.

(1)求证:EF//ABC平面;
(2)求直线BE与平面CC1D夹角的正弦值;
(3)求平面A1CD与平面CC1D夹角的余弦值.
(1)取BB1的中点G,连接FG,EG,连接AD交EG于K,再连接FK.∵EK//A1 B1,且E是AA1的中点,∴K是AD的中点,∴FK//AC,EG//AB,又FK⊄平面ABC,AC⊂平面ABC,∴FK//平面ABC,同理可得,EG//平面ABC,又FK∩EG=K,∴平面EFG//平面ABC,∴EF//平面ABC.(2)在直三棱柱ABC-A1 B1 C1中,AC⊥AB,则可建立如图所示的空间直角坐标系,∵AA1=AB=AC=2,D为A1 B1的中点,E为AA1的中点,F为CD的中点,∴B(2,2,0),E(1,0,0),C(2,0,2),C1 (0,0,2),D(0,1,0)(BE) →=(-1,-2,0),(CC1 ) →=(-2,0,0),(CD) →=(-2,1,-2),设n →=(x...
查看完整答案在∆ABC中,a=√6,b=2c,cosC=-1/4.(1)求∠C的大小;(2)求sinB的值;(3)求sin(2A-B)的值.
定义函数f(x)代表|x|-2与x2-ax+3a-5中较小的数.若f(x)至少有3个零点,则a的取值范围为__________.
在∆ABC中,(CA)→=a,(CB)→=b,D是AC的中点,(CB)→=2(BE)→,试用a,b表示(DE)→=________;若(AB)→⊥DE→,求∠C的最大值为______.
52张扑克牌,没有大小王,无放回地抽取两次,则两次都抽到A的概率为______;已知第一次抽到的是A,则第二次抽到A的概率为______.
直线x-y+m=0(m>0)与圆(x-1)2+(y-1)2=3相交所得的弦长为m,则m=______.
设全集U={ -2, -1,0,1, 2} ,集合 A = {0,1, 2}, B = {-1,1},则A∩(CUB)=【 】
如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.
如图,在三棱锥S-ABC中,S在底面上的射影N位于底面的高CD上;M是侧棱SC上的一点,使截面MAB与底面所成的角等于∠NSC,求证:SC垂直于截面MAB.
如图,已知二面角α-AB-β的平面角是锐角,C是平面α内的一点(它不在棱AB上),点D是点C在平面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么【 】.