已知正方体ABCD-A1 B1 C1 D1,点E为A1 D1的中点,直线B1 C1交平面CDE于点F.
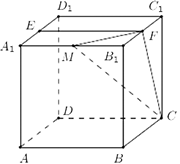
(1)求证:点F为B1 C1的中点;
(2)若点M为棱A1 B1上一点,且二面角M-CF-E的余弦值为 /3,求A1 M/A1B1 .
/3,求A1 M/A1B1 .
已知正方体ABCD-A1 B1 C1 D1,点E为A1 D1的中点,直线B1 C1交平面CDE于点F.

(1)求证:点F为B1 C1的中点;
(2)若点M为棱A1 B1上一点,且二面角M-CF-E的余弦值为 /3,求A1 M/A1B1 .
/3,求A1 M/A1B1 .
(1)因为ABCD-A1 B1 C1 D1为正方体,所以A1 D1//B1 C1,CD//C1 D1.又因为CD⊂平面ABCD,C1 D1⊂平面A1 B1 C1 D1,所以CD//平面A1 B1 C1 D1.因为平面CDEF∩平面A1 B1 C1 D1=EF,且CD⊂平面CDEF,所以CD//EF,故C1 D1//EF,所以四边形EFC1 D1为矩形,又点E为A1 D1的中点,故C1 F=D1 E=1/2 A1 D1=1/2 C1 B1,故点F为B1 C1的中点;(2) 因为ABCD-A1 B1 C1 D1为正方体,故DA,DC,DD1两两垂直.以D为坐标原点,分别以DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系...
查看完整答案如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若=a,=b,=c,则下列向量中与相等的向量是【 】
在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则【 】
已知 ABCD 是边长为 1 的正方形, 绕其中一条轴 AB 旋转成一个圆柱.(1) 求该圆柱的表面积;(2) 将 DC 旋转 90° 至 C1D1, 求线 C1D 与平面 ABCD 的夹角.
如图,在三棱锥S-ABC中,S在底面上的射影N位于底面的高CD上;M是侧棱SC上的一点,使截面MAB与底面所成的角等于∠NSC,求证:SC垂直于截面MAB.
如图,已知二面角α-AB-β的平面角是锐角,C是平面α内的一点(它不在棱AB上),点D是点C在平面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么【 】.
如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明:BC⊥AD;(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC.DE垂直平分SC,且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图,已知ABCD是边长为4的正方形,E,F分别是AB,AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
一间民房的屋顶有如图三种不同的盖法:①单向倾斜; ②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1,P2,P3. 若屋顶斜面与水平面所成的角都是α,则【 】
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则【 】