如图,在正方体ABCD-A1B1C1D1中E,F分别是BB1,CD的中点.
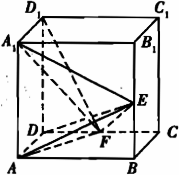
(Ⅰ)证明AD⊥D1F;
(Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明面AED⊥面A1FD1;
(Ⅳ)设AA1=2,求三棱锥F-A1ED1的体积VF-A1ED1.
如图,在正方体ABCD-A1B1C1D1中E,F分别是BB1,CD的中点.

(Ⅰ)证明AD⊥D1F;
(Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明面AED⊥面A1FD1;
(Ⅳ)设AA1=2,求三棱锥F-A1ED1的体积VF-A1ED1.
(Ⅰ)∵ AC1是正方体,∴AD⊥面DC1又D1 F⊂DC1,∴AD⊥D1 F.(Ⅱ)取AB中点G,连接A1 G,FG. 因为F是CD的中点,所以GE,AD平行且相等,又A1 D1,AD平行且相等,所以GE, A1 D1平行且相等,故GFD1 A1是平行四边形,A1 G//D1 F.设A1 G与AE相交于点H,则∠AHA1是AE与D1 F所成的角,因为E是BB1的中点、所以Rt△A1 AG≅Rt△ABE,∠GA1 A=∠GAH,从而∠AHA1=90°,即直线AE与D1 F所成...
查看完整答案如图,正三棱锥S-ABC的侧棱与底面边长相等,如果E,F分别为SC,AB的中点,那么异面直线EF与SA所成的角等于【 】
如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有【 】对。
如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S在底面射影O在△ABC内,那么O是△ABC的【 】。
已知四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为36π,且3≤l≤3√3,则该四棱锥体积的取值范围是【 】
在四棱锥P-ABCD中,PD⊥底面ABCD,CD//AB,AD=DC=CB=1,AB=2,DP=√3. (1)证明:BD⊥PA;(2)求PD与平面PAB所成的角的正弦值.
如果正方体ABCD-A′B′C′D′的棱长为a,则A′-ABD的体积是【 】
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则【 】