在四棱锥P-ABCD中,PD⊥底面ABCD,CD//AB,AD=DC=CB=1,AB=2,DP=√3.
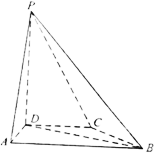
(1)证明:BD⊥PA;
(2)求PD与平面PAB所成的角的正弦值.
在四棱锥P-ABCD中,PD⊥底面ABCD,CD//AB,AD=DC=CB=1,AB=2,DP=√3.

(1)证明:BD⊥PA;
(2)求PD与平面PAB所成的角的正弦值.
(1)在四边形ABCD中,作DE⊥AB于E,CF⊥AB于F,因为CD//AB,AD=CD=CB=1,AB=2,所以四边形ABCD为等腰梯形,所以,AE=BF=1/2,故DE=√3/2,BD==√3,所以AD2+BD2=AB2,所以AD⊥BD,因为PD⊥平面ABCD,BD⊂平面ABCD,所以PD⊥BD,又PD∩AD=D,所以BD⊥平面PAD,又因PA⊂平面PAD,所以BD⊥PA.(2)如图...
查看完整答案如图,四棱锥P-ABCD 的底面是矩形,PD⊥底面ABCD,PD = DC = 1,M 为 BC 的中点,且 PB⊥AM.(1) 求 BC;(2) 求二面角A-PM-B的正弦值.
如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为【 】
在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则【 】
甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S甲和S乙,体积分别为V甲和V乙.若S甲/S乙 =2,则V甲/V乙 =【 】
已知a=31/32,b=cos1/4,c=4 sin1/4,则【 】
为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是【 】
在一个正方体中,过顶点A的三条棱的中点分别为E,F,G,该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如右图所示,则相应的侧视图是【 】
将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,,则三棱锥D-ABC的体积为【 】
已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小是【 】
在正三棱锥ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成的角的大小为【 】
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=1/2. (I)求四棱锥S-ABCD的体积;(Ⅱ)求面SCD与面SBA所成二面角的正切值.
已知四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为36π,且3≤l≤3√3,则该四棱锥体积的取值范围是【 】
如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E是PB的中点.(1)求证:OE//平面PAC;(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】