一个五面体ABC-DEF，已知AD∥BE∥CF，且两两之间距离为1，并已知AD=1,BE=2,CF=3，则该五面体的体积为【 】

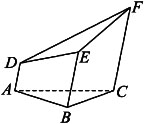
A、√3/6

B、3√3/4+1/2

C、√3/2

D、3√3/4-1/2

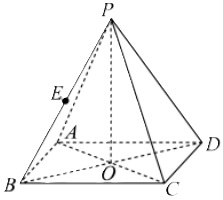
如图，正四棱锥P-ABCD,O为底面ABCD的中心.

(1)若AP=5,AD=3√2，求△POA绕PO旋转一周形成的几何体的体积；

(2)若AP=AD,E为PB的中点，求直线BD与平面AEC所成角的大小.

汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器，其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为 10 的等比数列，底面直径依次为 65mm,325mm,325mm，且斛量器的高为230mm，则斗量器的高为______mm，升量器的高为______mm.

以边长为4的正方形为底面的四棱锥，四条侧棱分别为4,4,2√2,2√2，则该四棱锥的高为【 】

A、√2/2

B、√3/2

C、2√3

D、√3

已知圆台甲、乙的上底面半径均为r₁，下底面半径均为r₂，圆台的母线长分别为2(r₂-r₁ ),3(r₂-r₁)，则圆台甲、乙的体积之比为______.