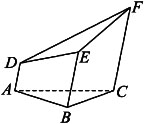
一个五面体ABC-DEF,已知AD∥BE∥CF,且两两之间距离为1,并已知AD=1,BE=2,CF=3,则该五面体的体积为【 】
A、√3/6
B、3√3/4+1/2
C、√3/2
D、3√3/4-1/2
一个五面体ABC-DEF,已知AD∥BE∥CF,且两两之间距离为1,并已知AD=1,BE=2,CF=3,则该五面体的体积为【 】

A、√3/6
B、3√3/4+1/2
C、√3/2
D、3√3/4-1/2
C
【解析】
解答过程见word版
以边长为4的正方形为底面的四棱锥,四条侧棱分别为4,4,2√2,2√2,则该四棱锥的高为【 】
如图,正四棱锥P-ABCD,O为底面ABCD的中心.(1)若AP=5,AD=3√2,求△POA绕PO旋转一周形成的几何体的体积;(2)若AP=AD,E为PB的中点,求直线BD与平面AEC所成角的大小.
如图所示三棱锥,底面为等边△ABC,O为AC中点,PO⊥平面ABC,AP=AC=2.(1)求三棱锥P-ABC的体积;(2)若M为BC中点,求PM与平面PAC所成角的大小.
P -ABC 为一正三角锥,其底面三角形 ABC 正三角形之每边为 10 尺,而APB、BPC、CPA 三个面角均为 30°,求此三角锥之高.
设一四面体有一三面角与另一四面体的一三面角对称,求证:其体积之比等于此两三面角三棱分别的乘积之比.
如图,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,,PA,BC的公垂线,ED=h.求证:三棱锥P-ABC的体积V=l2h/6.
如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有【 】对。
如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S在底面射影O在△ABC内,那么O是△ABC的【 】。
已知正三棱台ABC-A1B1C1的体积为52/3,AB=6,A1B1=2,则A1A与平面ABC所成角的正切值为【 】
已知圆台甲、乙的上底面半径均为r1,下底面半径均为r2,圆台的母线长分别为2(r2-r1 ),3(r2-r1),则圆台甲、乙的体积之比为______.
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点,则【 】
如图,已知长方体的对角线长为l,它与底面所成的角为α,底面两条对角线的夹角为β.求长方体的积体.
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
如图,四边形ABCD为正方形, ED⊥平面ABCD,FB//ED,AB=ED=2FB,记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则【 】