如图所示三棱锥,底面为等边△ABC,O为AC中点,PO⊥平面ABC,AP=AC=2.
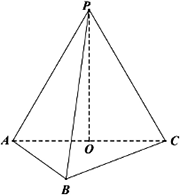
(1)求三棱锥P-ABC的体积;
(2)若M为BC中点,求PM与平面PAC所成角的大小.
已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O-ABC的体积为【 】
如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1) 证明:平面PAM⊥平面 PBD;(2) 若PD=DC=1,求四棱锥P-ABCD 的体积.
如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E是PB的中点.(1)求证:OE//平面PAC;(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
已知正三棱锥P-ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合.设集合T={ Q∈S|PQ≤5},则T表示的区域的面积为【 】
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
已知正三棱台上底面边长为2,下底面边长为4,且侧棱与底面所成的角是45°,那么这个正三棱台的体积等于__________.
已知圆台的上、下底面半径分别为r,2r,侧面积等于上、下底面积之和,则圆台的高为_______.
长方体的全面积为11,12条棱长度之和为24,则这个长方体的一条对角线长为【 】
建造一个容积为8m3,深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为________元。
已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为【 】
圆台上、下底面积分别为π,4π侧面积为6π,这个圆台的体积是【 】
如果棱台的两底面积分别是S,S',中截面的面积是S0,那么【 】
向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图像如图所示,那么水瓶的形状是【 】
如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为【 】
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC垂直于平面PBC.
如图,正四棱台中,A'D'所在的直线与BB'所在的直线是【 】
如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴oo'之间的距离等于______.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知:两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F,设A1E=m,AF=n. 求证:EF=.
已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如果直线l,m与平面α,β,γ满足:l=β∩γ,l//α,m⊂α和m⊥γ,那么必有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.