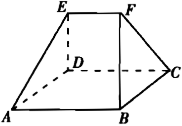
如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF//AB,EF=3/2，EF与面AC的距离为2，则该多面体的体积为【 】
A、9/2
B、5
C、6
D、15/2
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
直线x + y - 2 = 0截圆x2 + y2 = 4得到的劣弧所对的圆心角为【 】
若(2x+)4 = a0 + a1x + a2x2 + a3x3 + a4x4，则(a0 + a2 + a4 )2 - (a1 + a3 )2的值为【 】
若干毫升水倒人底面半径为2cm的圆柱形器皿中，量得水面的高度为6cm,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是【 】
若f(x)sinx是周期为π的奇函数，则f(x)可以是【 】
函数f(x)=M sin(ωx+φ) (ω>0)在区间[a,b]上是增函数，且f(a)=-M,f(b)=M，则函数g(x)=M cos(ωx+φ)在[a,b]上【 】
若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0，则g(b)等于【 】
已知映射f:A→B，其中，集合A={-3,-2,-1,1,2,3,4}，集合B中的元素都是A中元素在映射f下的象，且对任意的a∈A，在B中和它对应的元函数是|a|则集合B中元素的个数是【 】
一个正三棱台的下底和上底的周长分别为30cm和12cm，且侧面积等于两底面积之差，求斜高.
如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积.
如图，已知：在直三棱柱ABC-A1B1C1中，∠ACB = 90°，∠BAC=30°,BC=1,AA1= ,M是 CC1 的中点.求证AB1⊥A1M.
正三棱台高为1，上下底边长分别为3√3和4√3，所有顶点在同一球面上，则球的表面积是【 】
一个四面体的所有棱长都为√2，四个顶点在同一球面上，则此球的表面积为【 】
在正四棱台ABCD-A1B1C1D1中，AB=2,A1B1=1,AA1=√2，则该棱台的体积为______.
底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为______.
已知 A, B, C 为球 O 的球面上的三个点， ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π， AB = BC =AC = OO1，则球 O 的表面积为 【 】
向高为H的水瓶中注水，注满为止.如果注水量V与水深h的函数关系的图像如图所示,那么水瓶的形状是【 】
如下图所示,在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB, 将剩余部分沿OC,OD折叠，使OA,OB重合，则A(B),C,DCO为顶点的四面体的体积是_______.
设正多面体每个顶点连有M条棱，每面都是正N边形，则正整数M和N满足关系：M>2，N>2，MN<2(M+N)，这种正多面体共有【 】种。
在极坐标系中，椭圆的两焦点分别在极点和点(2c,0)，离心率为e，则它的极坐标方程是【 】
椭圆的极坐标方程为ρ=3/(2-cosθ )，则它在短轴上的两个顶点的极坐标是【 】
已知直线的极坐标方程为ρsin(θ+π/4)=/2，则极点到该直线的距离是______.
设直线(l)的参数方程是 (t是参数)椭圆(E)的参数方程是 (θ是参数)问：a,b应满足什么条件，使得对于任意m值来说，直线(l)与椭圆(E)总有公共点？