如下图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB, 将剩余部分沿OC,OD折叠,使OA,OB重合,则A(B),C,DCO为顶点的四面体的体积是_______.
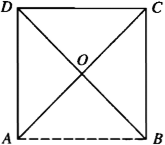
如下图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB, 将剩余部分沿OC,OD折叠,使OA,OB重合,则A(B),C,DCO为顶点的四面体的体积是_______.

8 /3
/3
将直线l1:nx+y-n=0 , l2:x+ny-n=0(n∈N*), x轴,y轴围成的封闭区域的面积记为Sn,则Sn= ________.
在n行n列矩阵中,记位于第i行第j列的数为 aij (i,j=1,2,...,n).当n=9时,a11+a22+a33+...a99=________.
从一副混合后的扑克牌(52张)中,随机抽取1张,事件A为“抽得红桃K”,事件B为“抽得黑桃”,则概率P(A∪B)= ________(结果用简分数表示).
对任意不等于1的正数a,函数f(x)=loga( x+3)的反函数的图像都经过点P,则点P的坐标为______.
随机变量ξ的概率分布律由下表给出: 该随机变量ξ的均值是______.
圆C:x2+y2-2x-4y+4=0的圆心到直线3x+4y+4=04的距离d=_____.