如图, D 为圆锥的顶点, O 是圆锥底面的圆心, △ABC 是底面的内接正三角形, P 为 DO 上一点, ∠APC = 90°.
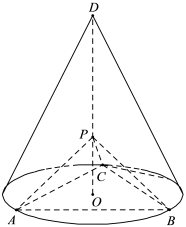
(1) 证明: 平面 PAB ⊥ 平面 PAC;
(2) 设 DO = 
, 圆锥的侧面积为
π, 求三棱锥 P − ABC 的体积.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2020年新高考Ⅰ·文）
答案解析
(1) 由题设可知, PA = PB = PC.由于 △ABC 是正三角形, 故可得 △PAC ≌ △PAB, △PAC ≌ △PBC.又 ∠APC = 90°, 故 ∠APB = 90°, ∠BPC = 90°. 从而 PB ⊥ PA, PB ⊥PC, 故 PB ⊥ 平面 PAC, 所以平面 PAB ⊥ 平面 PAC.(2) 设圆锥的底面半...
查看完整答案讨论
数列 {an} 满足 an+2 + (−1)nan = 3n − 1, 前 16 项和为 540, 则 a1 = ______.
曲线 y = lnx + x + 1 的一条切线的斜率为 2, 则该切线的方程为 ________________.
设向量 a = (1, −1), b = (m + 1, 2m − 4), 若 a ⊥ b, 则 m =______ .
已知 A, B, C 为球 O 的球面上的三个点， ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π， AB = BC = AC = OO1，则球 O 的表面积为【 】
设 F1, F2 是双曲线 C : x2 −y2/3 = 1 的两个焦点, O 为坐标原点, 点 P 在 C 上且 |OP| = 2, 则 △PF1F2 的 面积为【 】
设 {an} 是等比数列, 且 a1 + a2 + a3 = 1, a2 + a3 + a4 = 2, 则 a6 + a7 + a8 =【 】
若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的侧面积是________.
若一个圆锥的轴截面是等边三角形，其面积为，则这个圆锥的全面积是【 】
已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为【 】
已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为________.
甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S甲和S乙，体积分别为V甲和V乙．若S甲/S乙 =2，则V甲/V乙 =【 】
有圆锥高8寸，底之半径4寸，今距顶点 2寸之处，作与底平行之平面截断此圆锥，问此两部分之体积各几何?
已知圆锥的顶点为P，底面圆心为O,AB为底面直径，∠APB=120°,AP=2，点C在底面圆周上，且二面角P-AC-O为45°，则【 】
已知圆锥面x²+y²=z²/3，记沿该圆锥面从P(-√3,3,6)到Q(√3,0,3)的曲线长度的最小值为I，则[10I]=________.
在长方体ABCD-A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B所成的角均为30°，则【 】
在四棱锥P-ABCD中，PD⊥底面ABCD,CD//AB,AD=DC=CB=1,AB=2,DP=√3． （1）证明：BD⊥PA；（2）求PD与平面PAB所成的角的正弦值．
在正方体ABCD-A1B1C1D1中，E，F分别为AB,BC的中点，则【 】
已知正三棱锥P-ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={ Q∈S|PQ≤5}，则T表示的区域的面积为【 】
如图所示三棱锥，底面为等边△ABC，O为AC中点，PO⊥平面ABC，AP=AC=2.(1)求三棱锥P-ABC的体积;(2)若M为BC中点，求PM与平面PAC所成角的大小.
设正多面体每个顶点连有M条棱，每面都是正N边形，则正整数M和N满足关系：M>2，N>2，MN<2(M+N)，这种正多面体共有【 】种。
有长方体积之冰块，其长 2 步，阔 1 步 3 尺，厚4 尺，而此冰之比重为 0.93，若置其于水中，浮出水面之高几寸?