高中数学-高考试题(新高考Ⅰ 2020年程序框图)

单项选择（2020年新高考Ⅰ·文）

执行如图的程序框图，则输出的 n =【】

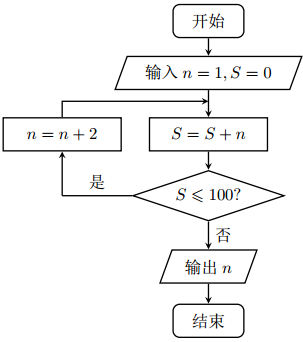
A、17

B、19

C、21

D、23

答案解析

C

讨论

高中数学

设 alog34 = 2, 则 4−a =【】

已知圆 x2 + y2 −6x = 0, 过点 (1,2) 的直线被该圆所截得的弦的长度的最小值为【】

设O为正方形 ABCD 的中心, 在 O,A,B,C,D 中任取 3 点, 则取到的 3 点共线的概率为【】

若 z = 1 + 2i+i3, 则|z| =【】

已知集合 A = {x | x2 −3x−4 < 0},B = {−4,1,3,5}, 则 A∩B=【】

已知数列{an}满足：a1=1，a2=4,且an2 - an-1an+1=2n-1(n≥2,n∈N*)，求a2020的个位数.

已知x,y,z>0，判断s=x/(x+y) + y/(y+z) + z/(z+x) 是否存在最大值与最小值.

求19x+93y=4xy的整数解的组数.

已椭圆 +y2 =1，圆x2 + y2=4，从圆上一点作椭圆的切点弦，求切点弦所围成的面积.

若f(x)=x5+px+q有有理根，且正整数p,q不大于100，则满足条件的(p,q)共有几组.

算法初步

如图是一个算法流程图, 若输出 y 的值为 −2, 则输入 x 的值是______.

执行下面的流程图，输出的n=【】

执行如图的程序框图, 若输入 k = 0, a = 0, 则输出的 k 为【】

对任意函数f(x),x∈D，可按图示构造一个数列发生器，其工作原理如下：①输入数据x0∈D，经数列发生器输出x1=f(x0 )；②若x1∉D，则数列发生器结束工作；若x1∈D，将x1反馈回输入端，再输出x2=f(x1 )，并依此规律继续下去，现定义f(x)=(4x-2)/(x+1). （Ⅰ）若输入x0=49/65，则由数列发生器产生数列{xn }，请写出数列{xn }的所有项；（Ⅱ）若要数列发生器生产一个无穷的常数数列，试求输入的初始数据x0的值.（Ⅲ）若输入x0时，产生的无穷数列{xn }满足：对任意正整数n，均有xn<xn+1，求x0的取值范围.

2010年上海世博会园区每天9:00开园，20:00停止入园.在下面的框图中，S表示上海世博会官方网站在每个整点报道的入园总人数，a表示整点报道前1个小时内入园人数，则空白的执行框内应填入__________.

一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯（卫生习惯分为良好和不够良好两类）的关系，在已患该疾病的病例中随机调查了100例（称为病例组），同时在未患该疾病的人群中随机调查了100人（称为对照组），得到如下数据：不够良好良好病例组 40 60对照组 10 90（1）能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异？（2）从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”．(P(B|A))/(P(B ̄|A))与(P(B|A ̄))/(P(B ̄|A ̄))的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标，记该指标为R．（ⅰ）证明：R=P(A|B)/P(A ̄|B)⋅P(A ̄|B ̄)/P(A|B ̄)；（ⅱ）利用该调查数据，给出P(A|B),P(A|B ̄)的估计值，并利用（ⅰ）的结果给出R的估计值．附：K2=n(ad-bc)2/((a+b)(c+d)(a+c)(b+d))，P(K2≥k) 0.050 0.010 0.001k 3.841 6.635 10.828

有一组样本数据x1,x2,⋯,x6，其中x1是最小值，x6是最大值，则【】

甲乙两人投篮, 每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮. 无论之前投篮情况如何, 甲每次投篮的命中率均为 0.6，乙每次投篮的命中率均为0.8，由抽签决定第一次投篮的人选，第一次投篮的人是甲、乙的概率各为0.5.(1)求第2次投篮的人是乙的概率；(2)求第i次投篮的人是甲的概率；(3)已知：若随机变量X_i服从两点分布，且P(Xi=1)=1-P(Xi=0)=qi,i=1,2,⋯,n，则E(Xi )=qi ，记前n次（即从第1次到第n次投篮）中甲投篮的次数为Y，求E(Y).

某校一个课外学习小组为研究某作物种子的发芽率 y 和温度 x (单位: °C) 的关系, 在 20 个不同的温度条件下进行种子发芽实验, 由实验数据 (xi, yi) (i = 1, 2, · · · , 20) 得到下面的散点图:由此散点图, 在 10°C 至 40°C 之间, 下面四个回归方程类型中最适宜作为发芽率 y 和温度 x 的回归方程类型的是【】。

已知 F 为双曲线 C : =1 (a > 0, b > 0) 的右焦点, A 为 C 的右顶点, B 为 C 上的点, 且 BF垂直于 x 轴. 若 AB 的斜率为 3, 则 C 的离心率为 __________.

程序框图

在直角坐标系 xOy 中, 曲线 C1 的参数方程为 (t 为参数). 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 曲线 C2 的极坐标方程为 4ρcosθ−16ρsinθ + 3 = 0.(1) 当 k = 1 时, C1 是什么曲线?(2) 当 k = 4 时, 求 C1 与 C2 的公共点的直角坐标.

某学校组织“一带一路”知识竞赛，有A，B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束.A类问题中的每个问题回答正确得20分，否则得0分;B类问题中的每个问题回答正确得80分，否则得0分.已知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关.(1)若小明先回答A类问题，记X为小明的累计得分，求X的分布列；(2)为使累计得分的期望最大，小明应选择先回答哪类问题?并说明理由。

从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为【】

已知函数f(x)=a(ex+a)-x.（1）讨论f(x)的单调性；（2）证明：当a>0时，f(x)>2lna+3/2.

若 z = 1 +i，则|z2 −2z| =【】

函数 f(x) = x4 − 2x3 的图像在点 (1, f(1)) 处的切线方程为【】。

若i(i-z)=1，则z ̅+z=【】

已知z=(1-i)/(2+2i)，则z-z ̅=【】

甲、乙、丙三位同学进行羽毛球比赛, 约定赛制如下:累计负两场者被淘汰; 比赛前抽签决定首先比赛的两人, 另一人轮空; 每场比赛的胜者与轮空者进行下一场比赛, 负者下一场轮空, 直至有一人被淘汰; 当一人被淘汰后, 剩余的两人继续比赛, 直至其中一人被淘汰, 另一人最终获胜, 比赛结束.经抽签, 甲、乙首先比赛, 丙轮空. 设每场比赛双方获胜的概率都为 1/2.(1) 求甲连胜四场的概率;(2) 求需要进行第五场比赛的概率;(3) 求丙最终获胜的概率.

已知z=2-i，则z(z ̅+i)=【】