执行下面的流程图,输出的n=【 】
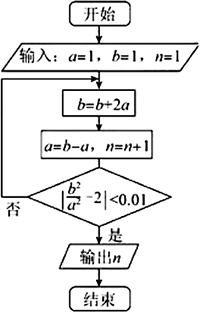
A、3
B、4
C、5
D、6
执行下面的流程图,输出的n=【 】

A、3
B、4
C、5
D、6
B第一次循环:b=1+1×2=3,a=3-1=2,n=1+1=2,|b2/a2 -2|=|(3/2)2-2|=1/4>0.01第二次循环:b=3+2×2=7,a=7-2=5,n=2+1=3,|b2/a2 ...
查看完整答案设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=【 】
已知向量a,b满足|a|=1,|b|=√3,|a-2b|=3,则a⋅b=【 】
已知z=1-2i,且z+az ̄+b=0,其中a,b为实数,则【 】
设全集U={1,2,3,4,5},集合M满足∁UM={1,3},则【 】
已知函数f(x)=x3-x,g(x)=x2+a,曲线y=f(x)在点(x1,f(x1))处的切线也是曲线y=g(x)的切线.(1)若x1=-1,求a;(2)求a的取值范围.
记双曲线C:x2/a2 -y2/b2 =1(a>0,b>0)的离心率为e,写出满足条件“直线y=2x与C无公共点”的e的一个值_________.
如图,四棱锥P-ABCD 的底面是矩形,PD⊥底面ABCD,PD = DC = 1,M 为 BC 的中点,且 PB⊥AM.(1) 求 BC;(2) 求二面角A-PM-B的正弦值.
记Sn为数列{an}的前n项和,bn为数列{Sn}的前n项积,已知2/Sn +1/bn =2.(1)证明:数列{bn}是等差数列;(2)求{an}的通项公式.
设2(z+z ̅)+3(z - z ̅)=4+6i,则z=【 】
将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有【 】
设函数f(x)=(1-x)/(1+x),则下列函数中为奇函数的是【 】
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍,纵坐标不变,再把所得曲线向右平移π/3个单位长度,得到函数sin(x-π/4)的图像,则f(x)=【 】