在直角坐标系xOy中,曲线C的方程为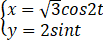 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立坐标系,已知直线l的极坐标方程为ρsin(θ+π/3)+m=0.
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立坐标系,已知直线l的极坐标方程为ρsin(θ+π/3)+m=0.
(1) 写出l的直角坐标方程;
(2) 若l与C有公共点,求m的取值范围.
在直角坐标系xOy中,曲线C的方程为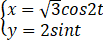 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立坐标系,已知直线l的极坐标方程为ρsin(θ+π/3)+m=0.
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立坐标系,已知直线l的极坐标方程为ρsin(θ+π/3)+m=0.
(1) 写出l的直角坐标方程;
(2) 若l与C有公共点,求m的取值范围.
(1)由ρ sin(θ+π/3)+m=0可得ρ(sinθ cosπ/3+cosθ sinπ/3 )+m=0,即ρ(1/2 sinθ+√3/2 cosθ)+m=0,1/2 y+√3/2 x+m=0,故l的方程为√3 x+y+2m=0.(2)由得,x=√3...
查看完整答案