曲线的参数方程是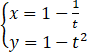 (t是参数,t≠0),它的普通方程是【 】
(t是参数,t≠0),它的普通方程是【 】
A、(x - 1)2(y-1)=1
B、y=x(x - 2)/(1 - x)2
C、y=1/(1 - x)2 -1
D、y=x/(1 - x2 )+1
曲线的参数方程是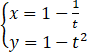 (t是参数,t≠0),它的普通方程是【 】
(t是参数,t≠0),它的普通方程是【 】
A、(x - 1)2(y-1)=1
B、y=x(x - 2)/(1 - x)2
C、y=1/(1 - x)2 -1
D、y=x/(1 - x2 )+1
B
长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是【 】
将y=2x的图像【 】,再作关于直线y=x对称的图像,可得到函数y=log2(x+1)的图像.
满足arccos(1-x)≥arccos的x的取值范围是【 】
函数y=sin(π/3 - 2x)+cos2x的最小正周期是【 】
已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小是【 】
函数y=tan(1/2 x - 1/3 π)在一个周期内的图像是【 】
如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a=【 】