-
关注“优题吧”，分配平台账号.
题吧，智能辅助学习中心
高考2003年全国旧课程( )
圆锥曲线ρ=8sinθ/cos2θ 的准线方程是【 】
A、ρcosθ=-2
B、ρcosθ=2
C、ρsinθ=-2
D、ρsinθ=2
ρsinθ=-2
将圆锥曲线的极坐标方程化为普通方程为：x2=8y，其准线方程为：y=-2，极坐标方程为：ρsinθ=-2.
高考2022年全国甲·理( )
在直角坐标系xOy中，曲线C1的参数方程为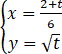
，（t为参数），曲线C2的参数方程为
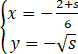，（s为参数）.
（1）写出C1的普通方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C3的极坐标方程为2cosθ-sinθ=0，求C3与C1交点的直角坐标，及C3与C2交点的直角坐标.
（1）由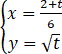，（t为参数），消去参数t可得C1的普通方程为y2=6x-2(y≥0)；
（2）由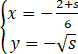，（s为参数），消去参数s可得C2的普通方程为y2=-6x-2(y≤0).
由2cosθ-sinθ=0得2ρcosθ-ρsinθ=0，所以曲线C3直角坐标方程为2x-y=0.
联立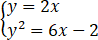
，解得
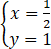或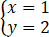
，
∴C3与C1交点的直角坐标为(1/2,1)与(1,2).
联立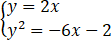
，解得
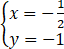或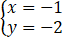
，
∴C3与C1交点的直角坐标为(1/2,1)与(1,2).
∴C3与C2交点的直角坐标为(-1/2,-1)与(-1,-2).
高考2021年北京市( )
若P(cosθ,sinθ)与Q(cos(θ+π/6),sin(θ+π/6))关于 y轴对称，写出一个符合题意的θ值________.
5π/12
高考2001年上海市( )
直线y=2x-1/2与曲线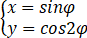
（φ为参数）的交点坐标是________.
(1/2,1/2)
高考2000年上海市( )
圆锥曲线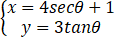
的焦点坐标是________.
(-4,0),(6,0)