已知 C1, C2 的参数方程分别为 C1 :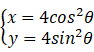 (θ为参数), C2 :
(θ为参数), C2 : 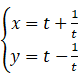 (t 为参数) ,
(t 为参数) ,
(1) 将 C1, C2 的参数方程化为普通方程;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 设 C1, C2 的交点为 P , 求圆心在极轴上, 且经过极点和 P 的圆的极坐标方程.
已知 C1, C2 的参数方程分别为 C1 :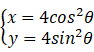 (θ为参数), C2 :
(θ为参数), C2 : 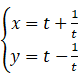 (t 为参数) ,
(t 为参数) ,
(1) 将 C1, C2 的参数方程化为普通方程;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 设 C1, C2 的交点为 P , 求圆心在极轴上, 且经过极点和 P 的圆的极坐标方程.
(1) C1 的普通方程为 x + y = 4(0 ⩽ x ⩽ 4).由 C2 的参数方程得 x2 = t2 + 1/t2 + 2, y2 = t2 + 1/t2 − 2, 所以 x2 − y2 = 4. 故 C2 的普通方程为 x2 − y2 ...
查看完整答案