如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .
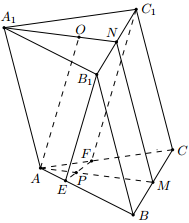
(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;
(2) 设 O 为 A1B1C1 的中心, 若 AO // 面 EB1C1F , 且 AO = AB, 求直线 B1E 与平面 A1AMN 所成角的正弦值.
如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .

(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;
(2) 设 O 为 A1B1C1 的中心, 若 AO // 面 EB1C1F , 且 AO = AB, 求直线 B1E 与平面 A1AMN 所成角的正弦值.
(1) 因为 M, N 分别为 BC, B1C1 的中点, 所以 MN // CC1 . 又由已知得 AA1 // CC1, 故 AA1 // MN.因为 △A1B1C1 是正三角形, 所以 B1C1⊥A1N. 又 B1C1⊥MN, 故 B1C1⊥平面A1AMN.所以平面 A1AMN⊥平面EB1C1F.(2) 由已知得 AM ⊥ BC. 以 M 为坐标原点, 的方向为 x 轴正方向, || 为单位长, 建立如图所示的空间直角坐标系 M − xyz, 则 AB = 2, AM = .连结 NP , 则四边形 AONP 为平行四...
查看完整答案△ABC 中, sin2A − sin2B − sin2C = sinBsinC.(1) 求 A;(2) 若 BC = 3, 求 △ABC 周长的最大值.
设复数 z1, z2 满足 |z1| = |z2| = 2, z1 + z2 = + i , 则 |z1 − z2| =______.
4 名同学到 3 个小区参加垃圾分类宣传活动, 每名同学只去 1 个小区, 每个小区至少安排 1 名学生, 则不同的安排方法有______种
己知单位向量 a, b 的夹角为 45°, ka − b 与 a 垂直, 则 k = ______.
已知 △ABC 是面积为(9)/4 的等边三角形, 且其顶点都在球 O 的球面上, 若球 O 的表面积为 16π, 则 O到平面 ABC 的距离为【 】
自一平面外之一点 A向平面上作 AB 垂线,CD 为平面内之任一线,AE线垂直于CD,证BE线垂直于CD.
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.
在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则【 】
在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为【 】
过一定点作一直线 AB 平行于一定平面 P,且与另一定平面 Q 所成之角等于定角 θ.
如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明:BC⊥AD;(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.
如图,已知正三棱柱ABC-A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F-BC-A的平面角为γ,则【 】
下列五个正方体图形中,l是正方体的一条对角线,点 M,N,P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是________(写出所有符合要求的图形序号).
已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体,其中两个面分别位于平面P1和P2上,下面哪条直线可能是该四面体的一条棱【 】
Find the equation of the projection of the linex=z+2,y=2z-4 upon the plane x+y- z = 0.