如图,直三棱柱ABC-A1 B1 C1的体积为4,△A1 BC的面积为2√2.
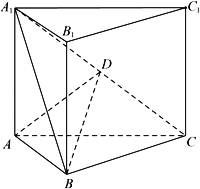
(1)求A到平面A1 BC的距离;
(2)设D为A1 C的中点,AA1=AB,平面A1 BC⊥平面ABB1 A1,求二面角A-BD-C的正弦值.
如图,直三棱柱ABC-A1 B1 C1的体积为4,△A1 BC的面积为2√2.

(1)求A到平面A1 BC的距离;
(2)设D为A1 C的中点,AA1=AB,平面A1 BC⊥平面ABB1 A1,求二面角A-BD-C的正弦值.
(1)在直三棱柱ABC-A1 B1 C1中,设点A到平面A1 BC的距离为h,则VA-A1BC=1/3 S△A1BC⋅h=(2√2)/3 h=VA1-ABC=1/3 S△ABC⋅A1 A=1/3 VABC-A1B1C1=4/3,解得h=√2,所以点A到平面A1 BC的距离为√2.(2)取A1 B的中点E,连接AE,如图,因为AA1=AB,所以AE⊥A1 B,又平面A1 BC⊥平面ABB1 A1,平面A1 BC∩平面ABB1 A1=A1 B,且AE⊂平面ABB1 A1,所以AE⊥平面A1 BC,在直三棱柱ABC-A1 B1 C1中,BB1⊥平面ABC,由BC⊂平面A1 BC,BC⊂平面ABC可得AE⊥BC,BB1⊥BC,又AE,BB1⊂平面ABB1 A1且相交,所...
查看完整答案在体积为V的斜三棱柱ABC-A'B'C'中,已知S是侧棱CC'上的一点,过点S,A,B的截面截得的三棱锥的体积为V1,那么过点S,A',B'的截面截得的三棱锥的体积为______.
如图,已知:在直三棱柱ABC-A1B1C1中,∠ACB = 90°,∠BAC=30°,BC=1,AA1= ,M是 CC1 的中点.求证AB1⊥A1M.
如图,已知A1B1C1-ABC是正三棱柱,D是AC的中点.(Ⅰ)证明AB1//平面DBC1;(Ⅱ)假设AB1⊥BC1,求以BC1为棱、DBC1与CBC1为面的二面角α的度数.
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=CC,则BD1与AF1所成的角的余弦值是【 】
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件____________时,有A1C⊥B1D1)(注:填上你认为正确的一-种条件即可,不必考虑所有可能的情形).
一个正三棱柱形的零件,它的高是10cm,底面边长是2cm,求它的体积.
如图, 六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的. 已知螺帽的底面正六边形边长为 2cm, 高 为 2cm, 内孔半径为 0.5cm, 则此六角螺帽毛坯的体积是 __________cm3.
如图,已知ABCD是边长为4的正方形,E,F分别是AB,AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
一间民房的屋顶有如图三种不同的盖法:①单向倾斜; ②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1,P2,P3. 若屋顶斜面与水平面所成的角都是α,则【 】
如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.
如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明:BC⊥AD;(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.