如图,已知A1B1C1-ABC是正三棱柱,D是AC的中点.
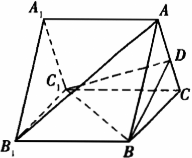
(Ⅰ)证明AB1//平面DBC1;
(Ⅱ)假设AB1⊥BC1,求以BC1为棱、DBC1与CBC1为面的二面角α的度数.
如图,已知A1B1C1-ABC是正三棱柱,D是AC的中点.

(Ⅰ)证明AB1//平面DBC1;
(Ⅱ)假设AB1⊥BC1,求以BC1为棱、DBC1与CBC1为面的二面角α的度数.
(I)证明: ∵A1B1C1-ABC是正三棱柱,∴四边形B1BCC1是矩形.连接B1C交BC1于E,则B1E=EC连接DE.在△AB1C中,∵AD=DC,∴DE//AB1.又AB1⊄平面DBC1,DE ⊂平面DBC1,∴AB1//平面DBC1.(Ⅱ)解:作DF⊥BC,垂足为F,则DF⊥面B1BCC1,连接EF,则EF是ED在平面B1BCC1上的射影.AB1⊥BC1,由(I)知AB1//DE,∴DE⊥BC1,则BC1⊥EF...
查看完整答案如图,已知:在直三棱柱ABC-A1B1C1中,∠ACB = 90°,∠BAC=30°,BC=1,AA1= ,M是 CC1 的中点.求证AB1⊥A1M.
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是【 】
如图, 六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的. 已知螺帽的底面正六边形边长为 2cm, 高 为 2cm, 内孔半径为 0.5cm, 则此六角螺帽毛坯的体积是 __________cm3.
如图,三棱柱ABC-A1B1C1中,若E,F分别为AB,AC的中点,平面EB1C1F将三棱柱分成体积为V1,V2的两部分,那么V1:V2=__________.
在体积为V的斜三棱柱ABC-A'B'C'中,已知S是侧棱CC'上的一点,过点S,A,B的截面截得的三棱锥的体积为V1,那么过点S,A',B'的截面截得的三棱锥的体积为______.
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件____________时,有A1C⊥B1D1)(注:填上你认为正确的一-种条件即可,不必考虑所有可能的情形).
在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为120°。若要光源恰好照亮整个广场,则其高度应为________(精确到0.1m)。
建造一个容积为8m3,深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为________元。
已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为【 】
如图,四边形ABCD为正方形, ED⊥平面ABCD,FB//ED,AB=ED=2FB,记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则【 】
已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,AP=2,点C在底面圆周上,且二面角P-AC-O为45°,则【 】
已知三个平面两两相交,有三条交线.求证这三条交线交于一点或互相平行.
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC垂直于平面PBC.
如图,正四棱台中,A'D'所在的直线与BB'所在的直线是【 】
如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴oo'之间的距离等于______.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知:两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F,设A1E=m,AF=n. 求证:EF=.