高中数学-高考试题(全国统考 1986年空间直线及关系)

证明题（1986年全国统考）

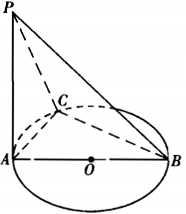
如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A，B的任意一点.

求证：平面PAC垂直于平面PBC.

答案解析

设圆O所在平面为α.由已知条件，PA⊥平面α，又BC在平面α内，所以PA⊥BC.因为∠BCA是直角，所以BC⊥AC.而PA与AC是△PAC所在平面内的相交直线，所以BC⊥△PAC所在的平面.从而证得△...

查看完整答案

讨论

高中数学

已知sinθ-cosθ=1/2，求sin3θ - cos3θ的值.

求(2x3-1/x2 )5展开式中的常数项.

全国统考数列极限

在xOy平面上，四边形ABCD的四个顶点坐标依次为(0,0),(1,0),(2,1)及(0,3).求这个四边形绕x轴旋转一周所得到的几何体的体积.

已知ω=(-1-i)/2，求ω2+ω+1的值.

全国统考指数函数

当x∈[0,1]时，在下面关系式中正确的是【】

在下列各图中，y=ax2+bx与y=ax+b (ab≠0)的图像只能是【】

在正方形SG1G2G3中，E，F分别是G1G2及G2G3的中点，D是EF中点. 现沿SE、SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G.那么，在四面体S-EFG中必有【】

如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)所表示的曲线关于y=x对称，那么必有【】

空间解析几何

直三棱柱ABC-A1B1C1中，AA1=AB=AC=2,AA1⊥AB,D为A1B1的中点，E为AA1的中点，F为CD的中点.(1)求证：EF//ABC平面；(2)求直线BE与平面CC1D夹角的正弦值；(3)求平面A1CD与平面CC1D夹角的余弦值.

如图，在正四棱柱ABCD-A1 B1 C1 D1中，AB=2,AA1=4，点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.(1)证明：B2 C2//A2 D2;(2)点P在棱BB1上，当二面角P-A2 C2-D2为150°时，求B2 P.

坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素，安装灯带可以勾勒出建筑轮廓，展现造型之美.如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形，若AB=25m,BC=AD=10m，且等腰梯形所在的平面、等腰三角形所在的平面与平面ABCD的夹角的正切值均为√14/5，则该五面体的所有棱长之和为【】

如图，在三棱锥P-ABC中，PA⊥平面ABC,PA=AB=BC=1,PC=√3. (1)求证：BC⊥平面PAB；(2)求二面角A-PC-B的大小.

如图，四棱锥P-ABCD中，PA⊥底面ABCD,PA=AC=2,BC=1,AB=√3. (Ⅰ)若AD⊥PB，证明：AD//平面PBC；(Ⅱ)若AD⊥DC，且二面角A-CP-D的正弦值为√42/7，求AD.

如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径, AE = AD. △ABC 是底面的内接正三角形,P 为 DO 上一点, PO = DO.(1) 证明: PA ⊥ 平面 PBC;(2) 求二面角 B − PC − E 的余弦值.

如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;(2) 设 O 为 △A1B1C1 的中心, 若 AO = AB = 6, AO//平面 EB1C1F , 且 ∠MPN = π/3 , 求四棱锥 B −EB1C1F 的体积.

如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.(1) 证明: 点 C1 在平面 AEF 内;(2) 若 AB = 2, AD = 1, AA1 = 3, 求二面角 A − EF − A1 的正弦值.

在三棱柱 ABC − A1B1C1 中, AB ⊥ AC, B1C ⊥ 平面 ABC, E, F 分别是 AC, B1C 的中点.(1) 求证: EF // 平面 AB1C1;(2) 求证: 平面 AB1C ⊥ 平面 ABB1.

直升飞机上一点 P 在地平面 M 上的正射影是 A ．从P看地平面上一物体 B （不同于 A ) ，直线P B 垂直于飞机窗玻璃所在的平面 N（如图）．证明：平面 N 必与平面 M 相交，且交线 l 垂直于 AB.

空间直线及关系

已知三个平面两两相交，有三条交线.求证这三条交线交于一点或互相平行.

已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体，其中两个面分别位于平面P1和P2上，下面哪条直线可能是该四面体的一条棱【】

Find the equation of the projection of the linex=z+2,y=2z-4 upon the plane x+y- z = 0.

Find the equation of the plane passing through the line (x-x1)/a1 =(y-y1)/b1 =(z-z1)/c1 which is parallel to the (x-x2)/a2 =(y-y2)/b2 =(z-z2)/c2 .

自一平面外之一点 A向平面上作 AB 垂线，CD 为平面内之任一线，AE线垂直于CD，证BE线垂直于CD.

过一定点作一直线 AB 平行于一定平面 P，且与另一定平面 Q 所成之角等于定角 θ.

如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;(2) 设 O 为 A1B1C1 的中心, 若 AO // 面 EB1C1F , 且 AO = AB, 求直线 B1E 与平面 A1AMN 所成角的正弦值.

日晷是中国古代用来测定时间的仪器, 利用与晷面垂直的晷针投射到晷面的影子来测定时间. 把地球看成一个球 (球心记为 O) , 地球上一点 A 的纬度是指 OA 与地球赤道所在平面所成角, 点 A 处的水平面是指过点 A 且与 OA 垂直的平面. 在点 A 处放置一个日晷, 若晷面与赤道所在平面平行, 点 A 处的纬度为北纬 40°, 则晷针与点 A 处的水平面所成角为【】

如图, 三棱台 ABC − DEF 中, 平面 ACFD ⊥ 平面 ABC, ∠ACB = ∠ACD = 45°, DC = 2BC.(I) 证明: EF ⊥ DB;(II) 求 DF 与面 DBC 所成角的正弦值.

在120°的二面角P-α-Q的两个面P和Q内，分别有点A和B . 已知点A和点B到棱α的距离分别为2和4，且线段AB=10.(1) 求直线AB和棱α所成的角；(2) 求直线AB和平面Q所成的角.