如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB=BC=1,PC=√3.
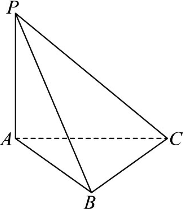
(1)求证:BC⊥平面PAB;
(2)求二面角A-PC-B的大小.
如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB=BC=1,PC=√3.

(1)求证:BC⊥平面PAB;
(2)求二面角A-PC-B的大小.
(1)∵PA⊥平面ABC,BC⊂平面ABC,∴PA⊥BC,同理PA⊥AB,∴△PAB为直角三角形,又∵PB=√2,BC=1,PC=√3,∴PB²+BC²=PC²,∴△PBC为直角三解形,BC⊥PB,又∵BC⊥PA,PA∩PB=P,∴BC⊥平面PAB.(2)由(1)知,BC⊥AB,以A为原点,AB为x轴,AP为z轴,建立空间直角坐标系,如图:则A(0,0,0),P(0,0,1),C(1,1,0),B(1,0,0),∴(AP)⇀=(0,0,1),(AC)⇀...
查看完整答案如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若=a,=b,=c,则下列向量中与相等的向量是【 】
在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则【 】
若直线2x+y-1=0是圆(x-a)2+y2=1的一条对称轴,则a=【 】
设{an}是公差不为0的无穷等差数列,则“{an}为递增数列”是“存在正整数N0,当n>N0时,an>0”的【 】
若(2x-1)4=a4 x4+a3 x3+a2 x2+a1 x+a0,则a0+a2+a4=【 】
已知正三棱锥P-ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合.设集合T={ Q∈S|PQ≤5},则T表示的区域的面积为【 】
在120°的二面角P-α-Q的两个面P和Q内,分别有点A和B . 已知点A和点B到棱α的距离分别为2和4,且线段AB=10.(1) 求直线AB和棱α所成的角;(2) 求直线AB和平面Q所成的角.
已知空间四边形ABCD中AB=BC,CD=DA,M,N,P,Q分别是边AB,BC,CD,DA的中点(如图).求证MNPQ是一个矩形.
已知三个平面两两相交,有三条交线.求证这三条交线交于一点或互相平行.
在xOy平面上,四边形ABCD的四个顶点坐标依次为(0,0),(1,0),(2,1)及(0,3).求这个四边形绕x轴旋转一周所得到的几何体的体积.