对于R²中任意两点(x₁,y₁ ),(x₂,y₂)，定义该两点之间的小数距离为：

√(‖x₁-x₂ ‖²+‖y₁-y₂ ‖² )

其中‖x‖表示实数x离最近整数的距离.求最大的实数r，使得平面上存在四个点，两两之间的小数距离均不小于r.

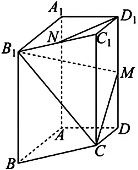
已知四棱柱ABCD-A₁ B₁ C₁ D₁中，底面ABCD为梯形，AB∥CD,AA₁⊥平面ABCD,AD⊥AB，其中AB=AA₁=2,AD=DC=1,N是B₁ C₁的中点，M是DD₁的中点.

(1)求证：D₁ N∥平面CB₁ M；

(2)求平面CB₁ M与平面BB₁ CC₁的夹角的余弦值；

(3)求点B到平面CB₁ M的距离.

设m,n为两条不同的直线，α为一个平面，则下列结论正确的是【 】

A、若m∥α,n⊂α，则m∥n

B、若m∥α,n∥α，则m∥n

C、若m∥α,n⊥α，则m⊥n

D、若m∥α,n⊥α，则m与n相交

定义一个集合Ω，集合元素是空间内的点集，任取P₁,P₂,P₃∈Ω，存在不全为0的实数λ₁,λ₂,λ₃，使得λ₁ (OP₁)+λ₂ (OP₂)+λ₃ (OP₃)=0.已知(1,0,0)∈Ω，则(0,0,1)∉Ω的充分条件是【 】

A、(0,0,0)∈Ω

B、(-1,0,0)∈Ω

C、(0,1,0)∈Ω

D、(0,0,-1)∈Ω

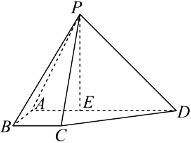
已知四棱锥P-ABCD,AD∥BC,AB=BC=1,AD=3,DE=PE=2,E是AD上一点，PE⊥AD.

(1)若F是PE的中点，证明：BF∥平面PCD.

(2)若AB⊥PED，求平面PAB与平面PCD的夹角的余弦值.