已知四棱柱ABCD-A1 B1 C1 D1中,底面ABCD为梯形,AB∥CD,AA1⊥平面ABCD,AD⊥AB,其中AB=AA1=2,AD=DC=1,N是B1 C1的中点,M是DD1的中点.
(1)求证:D1 N∥平面CB1 M;
(2)求平面CB1 M与平面BB1 CC1的夹角的余弦值;
(3)求点B到平面CB1 M的距离.
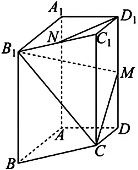
已知四棱柱ABCD-A1 B1 C1 D1中,底面ABCD为梯形,AB∥CD,AA1⊥平面ABCD,AD⊥AB,其中AB=AA1=2,AD=DC=1,N是B1 C1的中点,M是DD1的中点.
(1)求证:D1 N∥平面CB1 M;
(2)求平面CB1 M与平面BB1 CC1的夹角的余弦值;
(3)求点B到平面CB1 M的距离.

解答过程见word版
如图,已知A1B1C1-ABC是正三棱柱,D是AC的中点.(Ⅰ)证明AB1//平面DBC1;(Ⅱ)假设AB1⊥BC1,求以BC1为棱、DBC1与CBC1为面的二面角α的度数.
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=CC,则BD1与AF1所成的角的余弦值是【 】
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件____________时,有A1C⊥B1D1)(注:填上你认为正确的一-种条件即可,不必考虑所有可能的情形).
如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120°,腰为3的等腰三角形,则该几何体的体积为【 】
如图,三棱柱ABC-A1B1C1中,若E,F分别为AB,AC的中点,平面EB1C1F将三棱柱分成体积为V1,V2的两部分,那么V1:V2=__________.
在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成的角的大小为【 】