如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等边梯形,EF∥AD,BC∥AD,AD=4,AB=BC=EF=2,ED=√10,FB=2√3, M为AD的中点.
(1)证明:BM∥平面CDE;
(2)求点M到ABF的距离.
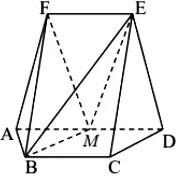
如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等边梯形,EF∥AD,BC∥AD,AD=4,AB=BC=EF=2,ED=√10,FB=2√3, M为AD的中点.
(1)证明:BM∥平面CDE;
(2)求点M到ABF的距离.

解答过程见word版
已知等比数列{an}的前n项和为Sn,且2Sn=3an+1-3.(1)求{an}的通项公式;(2)求数列{Sn}的通项公式.
曲线y=x³-3x与y=-(x-1)²+a在(0,+∞)上有两个不同的交点,则a的取值范围为 ______.
已知直线ax+y+2-a与圆C:x²+y²+4y-1=0交于A,B两点,则|AB|的最小值为【 】
函数f(x)=sinx-√3 cosx在[0,π]上的最大值是______.
曲线f(x)=x6+3x-1在(0,-1)处的切线与坐标轴围成的面积为【 】
甲、乙、丙丁四人排成一列,丙不在排头,且甲或乙在排尾的概率是【 】
等差数列{an}的前n项和为Sn,若S9=1,则a3+a7=【 】