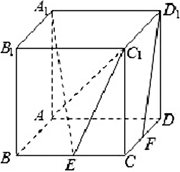
如图,在棱长为2的正方体ABCD-A1 B1 C1 D1中,E为棱BC的中点,F为棱CD的中点.
(1)求证:D1 F//平面A1 EC1;
(2)求直线AC1与平面A1 EC1所成角的正弦值;
(3)求二面角A-A1 C1-E的正弦值.
如图,在棱长为2的正方体ABCD-A1 B1 C1 D1中,E为棱BC的中点,F为棱CD的中点.

(1)求证:D1 F//平面A1 EC1;
(2)求直线AC1与平面A1 EC1所成角的正弦值;
(3)求二面角A-A1 C1-E的正弦值.
(1)如图所示,连接A1 C1,B1 D1相交于O,连接OE,EF,∵E为棱BC的中点,F为棱CD的中点,∴EF//B1 D1且EF=1/2 B1 D1,根据正方体的特性有OD1=1/2 B1 D1,∴四边形OEFD1为平行四边形,所以OE//D1 F,又∵OE⊂平面A1 EC1,D1 F⊄平面A1 EC1,∴D1 F//平面A1 EC1.(2)以A为坐标原点,AB,AD,AA1为坐标轴建立空间直角坐标系,如图所示,则:A(0,0,0),C1 (2,2,2),E(2,1,0),...
查看完整答案如图,正四棱台中,A'D'所在的直线与BB'所在的直线是【 】
如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴oo'之间的距离等于______.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知:两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F,设A1E=m,AF=n. 求证:EF=.
已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如果直线l,m与平面α,β,γ满足:l=β∩γ,l//α,m⊂α和m⊥γ,那么必有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.
下列五个正方体图形中,l是正方体的一条对角线,点 M,N,P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是________(写出所有符合要求的图形序号).
如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB=BC=1,PC=√3. (1)求证:BC⊥平面PAB;(2)求二面角A-PC-B的大小.
如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.
如图,在三棱锥S-ABC中,S在底面上的射影N位于底面的高CD上;M是侧棱SC上的一点,使截面MAB与底面所成的角等于∠NSC,求证:SC垂直于截面MAB.
如图,已知二面角α-AB-β的平面角是锐角,C是平面α内的一点(它不在棱AB上),点D是点C在平面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么【 】.
如图,四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB=,用α表示∠ASD,求sinα的值.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC.DE垂直平分SC,且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.