如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径, AE = AD. △ABC 是底面的内接正三角形,P 为 DO 上一点, PO =  DO.
DO.
(1) 证明: PA ⊥ 平面 PBC;
(2) 求二面角 B − PC − E 的余弦值.
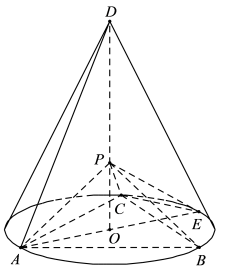
如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径, AE = AD. △ABC 是底面的内接正三角形,P 为 DO 上一点, PO =  DO.
DO.
(1) 证明: PA ⊥ 平面 PBC;
(2) 求二面角 B − PC − E 的余弦值.

(1) 设 DO = a, 由题设可得 PO =a,AO = a ,AB = a, PA = PB = PC = a. 因此PA2 + PB2 = AB2, 从而 PA ⊥ PB. 又 PA2 + PC2 = AC2, 故 PA ⊥ PC. 所以 PA ⊥ 平面 PBC.(2) 以 O 为坐标原点, 的方向为 y 轴正方向, || 为单位长,建立如图所示的空间直角坐标系 O-xyz.由题设可得...
查看完整答案设 {an} 是公比不为 1 的等比数列, a1 为 a2, a3 的等差中项.(1) 求 {an} 的公比;(2) 若 a1 = 1, 求数列 {nan} 的前 n 项和.
设 a, b 为单位向量, 且 |a + b| = 1, 则 |a − b| =__________.
若 x, y 满足约束条件 则 z = x + 7y 的最大值为 __________.
若 2a + log2a = 4b + 2log4b, 则【 】
已知 A, B, C 为球 O 的球面上的三个点, ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π, AB = BC =AC = OO1,则球 O 的表面积为 【 】