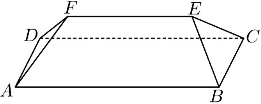
坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素,安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形,若AB=25m,BC=AD=10m,且等腰梯形所在的平面、等腰三角形所在的平面与平面ABCD的夹角的正切值均为√14/5,则该五面体的所有棱长之和为【 】
A、102m
B、112m
C、117m
D、125m
坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素,安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形,若AB=25m,BC=AD=10m,且等腰梯形所在的平面、等腰三角形所在的平面与平面ABCD的夹角的正切值均为√14/5,则该五面体的所有棱长之和为【 】

A、102m
B、112m
C、117m
D、125m
C如图,过E做EO⊥平面ABCD,垂足为O,过E分别做EG⊥BC,EM⊥AB,垂足分别为G,M,连接OG,OM.由题意得,等腰梯形所在的面、等腰三角形所在的面与底面的夹角分别为∠EMO,∠EGO,则tan∠EMO=tan∠EGO=√14/5.∵EO⊥平面ABCD,BC⊂平面ABCD,∴EO⊥BC.∵EG⊥BC,EO,EG⊂平面EOG,EO∩EG=E,∴B...
查看完整答案如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴oo'之间的距离等于______.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知:两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F,设A1E=m,AF=n. 求证:EF=.
已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如果直线l,m与平面α,β,γ满足:l=β∩γ,l//α,m⊂α和m⊥γ,那么必有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.
如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为【 】
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.
如图,在三棱锥S-ABC中,S在底面上的射影N位于底面的高CD上;M是侧棱SC上的一点,使截面MAB与底面所成的角等于∠NSC,求证:SC垂直于截面MAB.
如图,已知二面角α-AB-β的平面角是锐角,C是平面α内的一点(它不在棱AB上),点D是点C在平面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么【 】.
如图,四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB=,用α表示∠ASD,求sinα的值.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC.DE垂直平分SC,且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图,已知ABCD是边长为4的正方形,E,F分别是AB,AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.