高中数学-高考试题(全国统考 1989年空间直线及关系)

填空题（1989年全国统考）

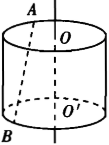
如图，已知圆柱的底面半径是3，高是4，A，B两点分别在两底面的圆周上，并且AB=5，那么直线AB与轴oo'之间的距离等于______.

答案解析

3/2

讨论

高中数学

已知A和B是两个命题，如果A是B的充分条件，那么B是A的______条件；A ̅是B ̅的______条件.

已知(1-2x)7=a0+a1 x+a2 x2+⋯+a7 x7，那么a1 x+a2+⋯+a7=__________.

函数y=(ex-1)/(ex+1)的反函数的定义域是__________.

不等式|x2-3x|>4的解集是____________.

方程sinx-cosx=的解集是____________________.

由数字1，2，3，4，5组成的没有重复数字的五位数，其中小于50000的偶数共有【】个

已知f(x)=8+2x-x2，如果g(x)=f(2-x2)，那么g(x)【】

如果双曲线x2/64-y2/36=1上一点P到它的右焦点的距离是8，那么点P到它的右准线的距离是【】

已知椭圆的极坐标方程是ρ=5/(3-2cosθ)，那么它的短轴长是【】

已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且相距为1，那么这个球的半径是【】

空间解析几何

Find the equation of the sphere which passes through (1,5,-3),(-3,0,0) which center on the 3x+y+z=0,x+2y +1 = 0.

Find the equation of the ruled surface whose generators are the system of the lines x-2y =4kx,k(x-2y)=4 and discuss the surface.

如图，四棱锥P-ABCD中，PA⊥底面ABCD,PA=AC=2,BC=1,AB=√3. (Ⅰ)若AD⊥PB，证明：AD//平面PBC；(Ⅱ)若AD⊥DC，且二面角A-CP-D的正弦值为√42/7，求AD.

如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径, AE = AD. △ABC 是底面的内接正三角形,P 为 DO 上一点, PO = DO.(1) 证明: PA ⊥ 平面 PBC;(2) 求二面角 B − PC − E 的余弦值.

如图, 已知三棱柱 ABC − A1B1C1 的底面是正三角形, 侧面 BB1C1C 是矩形, M, N 分别为 BC, B1C1 的中点, P 为 AM 上一点, 过 B1C1 和 P 的平面交 AB 于 E, 交 AC 于 F .(1) 证明: AA1 // MN, 且平面 A1AMN ⊥ 面 EB1C1F ;(2) 设 O 为 △A1B1C1 的中心, 若 AO = AB = 6, AO//平面 EB1C1F , 且 ∠MPN = π/3 , 求四棱锥 B −EB1C1F 的体积.

如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.(1) 证明: 点 C1 在平面 AEF 内;(2) 若 AB = 2, AD = 1, AA1 = 3, 求二面角 A − EF − A1 的正弦值.

如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.

如图, 在三棱柱 ABC − A1B1C1 中, CC1⊥平面 ABC, AC ⊥ BC, AC = BC = 2, CC1 = 3, 点 D, E 分别在棱 AA1 和棱 CC1 上, 且 AD = 1, CE = 2, M 为棱 A1B1 的中点.(I) 求证: C1M ⊥ B1D;(II) 求二面角 B − B1E − D 的正弦值;(III) 求直线 AB 与平面 DB1E 所成角的正弦值.

已知 ABCD 是边长为 1 的正方形, 绕其中一条轴 AB 旋转成一个圆柱.(1) 求该圆柱的表面积;(2) 将 DC 旋转 90° 至 C1D1, 求线 C1D 与平面 ABCD 的夹角.

如图，三棱锥A-BCD中，DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明：BC⊥AD;(2)点F满足(EF)→=(DA)→，求二面角D-AB-F的正弦值.

空间直线及关系

在棱长为a的正方体OABC-O'A'B'C'中，E,F分别是棱AB,BC上的动点，且AE=BF.（Ⅰ）求证：A'F⊥C'E；（Ⅱ）当三棱锥B'-BEF的体积取得最大值时，求二面角B'-EF-B的大小（结果用三角函数表示）.

求证两两相交而不过同一点的四条直线必在同一平面内.

在直棱柱A1B1C1-ABC中，∠BAC=π/2,AB=AC=AA1.已知G与E分别为A1B1和CC1的中点，D与F分别为线段AC和AB上的不动点（不包括端点）.若GD⊥EF，则线段DF的长度的取值范围为【】

已知正方体ABCD-A1B1C1D1，则【】

如图，已知正三棱柱ABC-A1B1C1,AC=AA1，E，F分别是棱BC,A1C1上的点．记EF与AA1所成的角为α，EF与平面ABC所成的角为β，二面角F-BC-A的平面角为γ，则【】

下列五个正方体图形中，l是正方体的一条对角线，点 M,N,P分别为其所在棱的中点，能得出l⊥面MNP的图形的序号是________(写出所有符合要求的图形序号).

已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体，其中两个面分别位于平面P1和P2上，下面哪条直线可能是该四面体的一条棱【】

Find the equation of the projection of the linex=z+2,y=2z-4 upon the plane x+y- z = 0.

Find the equation of the plane passing through the line (x-x1)/a1 =(y-y1)/b1 =(z-z1)/c1 which is parallel to the (x-x2)/a2 =(y-y2)/b2 =(z-z2)/c2 .

自一平面外之一点 A向平面上作 AB 垂线，CD 为平面内之任一线，AE线垂直于CD，证BE线垂直于CD.