如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.
(1) 证明: 点 C1 在平面 AEF 内;
(2) 若 AB = 2, AD = 1, AA1 = 3, 求二面角 A − EF − A1 的正弦值.
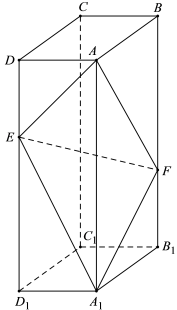
如图, 在长方体 ABCD − A1B1C1D1 中, 点 E, F 分别在棱 DD1, BB1 上, 且 2DE = ED1, BF = 2FB1.
(1) 证明: 点 C1 在平面 AEF 内;
(2) 若 AB = 2, AD = 1, AA1 = 3, 求二面角 A − EF − A1 的正弦值.

(1) 连结 C1F, 则 C1(0, 0, 0), A(a, b, c), E(a, 0, 2/3c), F(0, b, 1/3c), = (0, b, 1/3c), = (0, b, 1/3c), 得= , 因此 EA // C1F, 即 A, E, F, C1 四点共面, 所以点 C1 在平面 AEF 内.(2) 由已知得 A(2, 1, 3), E(2, 0, 2), F (0, 1, 1), A1(2, ...
查看完整答案设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.
已知 55 < 84, 134 < 85. 设 a = log53, b = log85, c = log138, 则【 】
若直线 l 与曲线 y = 和圆 x2 + y2 = 1/5 相切, 则 l 的方程为【 】
已知 2tanθ − tan(θ + π/4) = 7, 则 tanθ =【 】
在 △ABC 中, cosC = 2/3 , AC = 4, BC = 3, 则 cosB =【 】
已知向量 a, b 满足 |a| = 5, |b| = 6, a · b = −6, 则 cos⟨a, a + b⟩ =【 】
在一组样本数据中, 1, 2, 3, 4 出现的频率分别为 p1, p2, p3, p4, 且=1, 则下面四种情形中, 对应样本的标准差最大的一组是【 】