在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足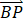 =λ
=λ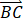 +μ
+μ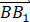 ,其中λ∈[0,1],μ∈[0,1],则【 】
,其中λ∈[0,1],μ∈[0,1],则【 】
A、当λ=1时,△AB1P的周长为定值
B、当μ=1时,三棱锥P-A1BC的体积为定值
C、当λ=1/2时,有且仅有一个点P,使得A1P⊥BP
D、当μ=1/2时,有且仅有一个点P,使得A1B⊥平面AB1P
在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足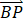 =λ
=λ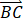 +μ
+μ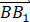 ,其中λ∈[0,1],μ∈[0,1],则【 】
,其中λ∈[0,1],μ∈[0,1],则【 】
A、当λ=1时,△AB1P的周长为定值
B、当μ=1时,三棱锥P-A1BC的体积为定值
C、当λ=1/2时,有且仅有一个点P,使得A1P⊥BP
D、当μ=1/2时,有且仅有一个点P,使得A1B⊥平面AB1P
BD
如图,已知A1B1C1-ABC是正三棱柱,D是AC的中点.(Ⅰ)证明AB1//平面DBC1;(Ⅱ)假设AB1⊥BC1,求以BC1为棱、DBC1与CBC1为面的二面角α的度数.
如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=CC,则BD1与AF1所成的角的余弦值是【 】
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件____________时,有A1C⊥B1D1)(注:填上你认为正确的一-种条件即可,不必考虑所有可能的情形).
在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成的角的大小为【 】
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是【 】
如图, 六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的. 已知螺帽的底面正六边形边长为 2cm, 高 为 2cm, 内孔半径为 0.5cm, 则此六角螺帽毛坯的体积是 __________cm3.
如图,三棱柱ABC-A1B1C1中,若E,F分别为AB,AC的中点,平面EB1C1F将三棱柱分成体积为V1,V2的两部分,那么V1:V2=__________.
在体积为V的斜三棱柱ABC-A'B'C'中,已知S是侧棱CC'上的一点,过点S,A,B的截面截得的三棱锥的体积为V1,那么过点S,A',B'的截面截得的三棱锥的体积为______.
已知 ABCD 是边长为 1 的正方形, 绕其中一条轴 AB 旋转成一个圆柱.(1) 求该圆柱的表面积;(2) 将 DC 旋转 90° 至 C1D1, 求线 C1D 与平面 ABCD 的夹角.
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点.求证:平面PAC垂直于平面PBC.
如图,正四棱台中,A'D'所在的直线与BB'所在的直线是【 】
如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴oo'之间的距离等于______.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知:两条异面直线a,b所成的角为θ,它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F,设A1E=m,AF=n. 求证:EF=.
已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如果直线l,m与平面α,β,γ满足:l=β∩γ,l//α,m⊂α和m⊥γ,那么必有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.