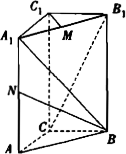
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是A1B1,A1A的中点.
(I)求 的长;
的长;
(II)求cos⟨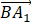 ,
,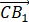 ⟩的值;
⟩的值;
(Ⅲ)求证A1B⊥C1M.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是A1B1,A1A的中点.

(I)求 的长;
的长;
(II)求cos⟨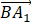 ,
,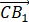 ⟩的值;
⟩的值;
(Ⅲ)求证A1B⊥C1M.
如图,以C为原点建立空间直角坐标系O-xyz. (I)依题意得B(0,1,0),N(1,0,1)∴||==(II)依题意得A1 (1,0,2),B(0,1,0),C(0,0,0),B1 (0,1,2).∴=(1,-1,2),=(0,1...
查看完整答案某厂生产电子元件,其产品的次品率为5%,现从一批产品中任意地连续取出2件,其中次数品数ξ的概率分布是ξ 0 1 2p
设集合A和B都是坐标平面上的点集{(x,y)|x∈R,y∈R},映射f:A→B把集合A中的元素(x,y)映射成集合B中的元素(x+y,x-y),则在映射f下,象(2,1)的原象是【 】
如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段AC 所成的比为λ,双曲线过C,D,E三点,且以A,B为焦点.当2/3≤λ≤3/4 时,求双曲线离心率e的取值范围.
设{cn},{bn}是公比不相等的两个比数列,cn =an+bn.证明数列{cn}不是等比数列.
已知数列{cn},其中cn=2n+3n,且数列{cn+1 - pcn}为等比数列,求常数p.
设函数f(x)= - ax,其中a>0.(I)解不等式f(x)≤1;(II)求a的取值范围,使函数f(x)在区间[0,+∞)上是单调函数.
已知 ABCD 是边长为 1 的正方形, 绕其中一条轴 AB 旋转成一个圆柱.(1) 求该圆柱的表面积;(2) 将 DC 旋转 90° 至 C1D1, 求线 C1D 与平面 ABCD 的夹角.
在xOy平面上,四边形ABCD的四个顶点坐标依次为(0,0),(1,0),(2,1)及(0,3).求这个四边形绕x轴旋转一周所得到的几何体的体积.
如图,已知二面角α-AB-β的平面角是锐角,C是平面α内的一点(它不在棱AB上),点D是点C在平面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么【 】.
如图,四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB=,用α表示∠ASD,求sinα的值.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC.DE垂直平分SC,且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图,已知ABCD是边长为4的正方形,E,F分别是AB,AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.