如图,平面四边形ABCD中,AB=8,CD=3,AD=5√3,∠ADC=90°,∠BAD=30°,点E,F满足(AE)→=2/5 (AD)→,(AF)→=1/2 (AB)→.将△AEF沿EF翻折至△PEF,使得PC=4√3.
(1)证明:EF⊥PD;
(2)求面PCD与面PBF所成二面角的正弦值.
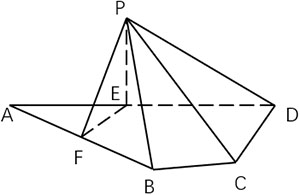
如图,平面四边形ABCD中,AB=8,CD=3,AD=5√3,∠ADC=90°,∠BAD=30°,点E,F满足(AE)→=2/5 (AD)→,(AF)→=1/2 (AB)→.将△AEF沿EF翻折至△PEF,使得PC=4√3.
(1)证明:EF⊥PD;
(2)求面PCD与面PBF所成二面角的正弦值.

解答过程见word版
设n为正整数.若平面中存在两点A,B及2024个不同的点P1,P2,⋯,P2024满足:线段AB及各条线段APi,BPi (i=1,2,⋯,2024)的长度均为不超过n的正整数,求n的最小值.
求最大的正整数n,使得平面上存在n个点P1,P2,⋯,Pn(任意三点不共线)和不过其中任意点的n条直线l1,l2,⋯,ln(任意三线不共点),满足对任意i≠j,直线Pi Pj,li,lj三线共点.
在平面直角坐标系xOy中,椭圆x²/a² +y²/b² =1(a>b>1)的右焦点为F(c,0),若存在经过焦点F的一条直线l交椭圆于A,B两点,使得OA⊥OB.求椭圆的离心率e=c/a的取值范围.
设a,b,c,d∈(0,1),满足a²+b²+c²+d²=3,证明:(1-a²)/(b+c)+(1-b²)/(c+d)+(1-c²)/(d+a)+(1-d²)/(a+b)<2/3.
如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB=BC=1,PC=√3. (1)求证:BC⊥平面PAB;(2)求二面角A-PC-B的大小.
如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点. (1)证明:BC⊥AD;(2)点F满足(EF)→=(DA)→,求二面角D-AB-F的正弦值.
如图,已知ABCD是边长为4的正方形,E,F分别是AB,AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
一间民房的屋顶有如图三种不同的盖法:①单向倾斜; ②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P1,P2,P3. 若屋顶斜面与水平面所成的角都是α,则【 】