设m,n为正整数且m≤n，证明：
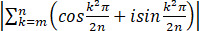≤m/n
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设n为正整数.若平面中存在两点A,B及2024个不同的点P1,P2,⋯,P2024满足：线段AB及各条线段APi,BPi (i=1,2,⋯,2024)的长度均为不超过n的正整数，求n的最小值.
求最大的正整数n，使得平面上存在n个点P1,P2,⋯,Pn(任意三点不共线)和不过其中任意点的n条直线l1,l2,⋯,ln(任意三线不共点)，满足对任意i≠j，直线Pi Pj,li,lj三线共点.
在平面直角坐标系xOy中，椭圆x²/a² +y²/b² =1(a>b>1)的右焦点为F(c,0)，若存在经过焦点F的一条直线l交椭圆于A,B两点，使得OA⊥OB.求椭圆的离心率e=c/a的取值范围.
设a,b,c,d∈(0,1)，满足a²+b²+c²+d²=3，证明：(1-a²)/(b+c)+(1-b²)/(c+d)+(1-c²)/(d+a)+(1-d²)/(a+b)<2/3.
对于函数f(x)=sin2x和g(x)=sin(2x-π/4)，下列正确的有【 】
已知α为第一象限角，β为第三象限角，tanα+tanβ=4,tanαtanβ=√2+1，则sin(α+β)=______.
设A+B+C=π，证明sinA+sinB+sinC=4 cos(A/2)cos(B/2)cos(C/2).
已知sin(α-β)=1/3,cosαsinβ=1/6，则cos(2α+2β)=【 】
已知α为锐角，cosα=(1+√5)/4，则sin(α/2)=【 】
已知π/2<β<α<3π/4,cos(α-β)=12/13,sin(α+β)=-3/5,求sin2α的值.
设α,β,γ为三角形内角，求证tg(α/2)∙tg(β/2)+tg(β/2)∙tg(γ/2)+tg(γ/2)∙tg(α/2)=1.
已知函数f(x)=sin(ωx+φ)，如图A,B是直线y=1/2与曲线y=f(x)的两个交点，若|AB|=π/6，则f(π)=________.
函数f(x)=M sin(ωx+φ) (ω>0)在区间[a,b]上是增函数，且f(a)=-M,f(b)=M，则函数g(x)=M cos(ωx+φ)在[a,b]上【 】
求函数y=(sinx+cosx)2+2cos2x的最小正周期.
下列区间中，函数f(x)=7sin(x-π/6)单调递增的区间是【 】
函数f(x)=sin x/3+cos x/3的最小正周期和最大值分别是【 】
已知f(x)=3sinx+2，对任意的x1∈[0,π/2]，都存在x2∈[0,π/2]，使得f(x1)=2f(x2+θ)+2成立，则下列选中θ可能的值是【 】