一项考试的可能得分为0,1,2,⋯,150,有100名考生P1,P2,⋯,P100,考完后依顺时针围成一圈交流成绩,记Pi的成绩为ai.每个考生Pi比较自己与相邻两人Pi-1,Pi+1(下标按模100理解 )的得分,定义Pi的激励值fi为:
fi=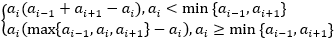
记S=f1+f2+⋯+f100.
(1)求S的最大值;
(2)求使得f1,f2,⋯,f100两两不相等的S的最大值.
一项考试的可能得分为0,1,2,⋯,150,有100名考生P1,P2,⋯,P100,考完后依顺时针围成一圈交流成绩,记Pi的成绩为ai.每个考生Pi比较自己与相邻两人Pi-1,Pi+1(下标按模100理解 )的得分,定义Pi的激励值fi为:
fi=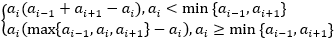
记S=f1+f2+⋯+f100.
(1)求S的最大值;
(2)求使得f1,f2,⋯,f100两两不相等的S的最大值.
解答过程见word版
求方程(√3+2sin2x)/(√3+2sinx)=√3 sinx+cos2x/2cosx在(0,π/2)内的解.
在锐角三角形△ABC中,AB>AC,O为外心. 设D为BC上一点,O1,O2分别为△ABD,△ACD的外心,△AO1O2的外接圆与⨀O交于不同于A的点L.证明:A,O,D三点共线当且仅当AL//BC.
已知函数f(x)=ex-ax-a3.(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若f(x)有极小值,且极小值小于0,求a的取值范围.
证明:任意正整数的平方均可表示为((a-b)²+(b-c)²+(c-a)²)/(2(ab+bc+ca))的形式,其中a,b,c为正整数.
设P为平面凸多边形,若线段AB的两端点在P的边界上,并且过A,B与AB垂直的两条直线之间的区域(含边界)包含P,则称线段AB为“锦弦”. 求最大的正整数k,使得任意平面凸多边形P都有k条锦弦.
记△ABC的内角A,B,C对应的边分别为a,b,c,已知sinA+√3 cosA=2.(1)求A.(2)若a=2,√2 bsinC=csin2B,求△ABC的周长.
在如图的4×4方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有____种选法,在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是______.
设函数f(x)=a(x+1)²-1,g(x)=cosx+2ax,当x∈(-1,1)时,曲线y=f(x)与y=g(x)恰有一个交点,则a=【 】
试求方程 3x³ + 8x² + 13x + 6 = 0 的根,已知一根为另两根倒数之和.
方程12x³-28x²+17x-3=0之根为a,b,c,已知b=a+1,求a,b,c.
设α,β为x²+mx+m²+a=0的二根,则α²+αβ+β²+a=0.
设a,b,c为方程x³+2x²+3x+4=0之根,求以a(1/b+1/c),b(1/c+1/a),c(1/a+1/b)为根之方程.