高中数学-高考试题(山西省 1949年解方程)

问答题（1949年山西省）

求以下两方程有公共根的条件：.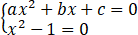

答案解析

暂无答案

讨论

高中数学

将f(x)=x³-3x²+5x+6的根增一常数，使变后的方程缺x²项.

若相相之二抛物线具有相同之顶点，且其主轴互相垂直，试证其公切线必与二抛物线各切于其通径之一端.

试证方程 x² + 6xy + 9y² + 4x + 12y -5 = 0 之轨迹为二平行直线.

若α,β,γ为方程x³+ax²+bx+c=0之根，试求行列式D=的值，但不许展开此行列式.

试求方程 3x³ + 8x² + 13x + 6 = 0 的根，已知一根为另两根倒数之和.

若n为正整数，试求(x+1/x)2n之展开式内x2n之系数.

若a1,a2,⋯,an为已知正数，试求atctan(a1-a2)/(1+a1 a2)+atctan(a2-a3)/(1+a2 a3)+⋯+atctan(an-1-an)/(1+an-1 an)的值.

求 cos20°cos40°cos80°的值.

有等高的两竿，自其底连线上一点望之，较近之竿的仰角为 60°，若自该点向此线之垂直方向行 80 尺而测之，得二竿之仰角为 45°，30°，试求二竿之高及其间的距离.

在定角 XOY 的二边上各取二点 P、Q，使 OP +OQ = a. 试求 PQ 的中点的轨迹.

解方程

解方程式3/x+6/(x-1)=(x+13)/(x(x-1))

中央政治学校解方程

北京大学解方程

求解方程式a³(b-c)(x -b)(x-c)+b³(c-a)(x-c)(x-a) +c³(a-b)(x-a)(x-b) =0且求其有等根之条件.

武汉大学解方程

解3x²-2x-5+9=0

解Ax+1/Bx-1 =C2x.

解2x³-3x²-3x+2=0

求方程式y5-5y4+9y3-9y2+5y-1=0之五根.

复旦大学解方程

函数

设a=2ln1.01,b=ln1.02,c=-1，则【】

已知f(x)=3/x+2，则f-1 (1)=__________.

已知一企业一年营业额1.1亿元，每年增加0.05亿元，利润0.16亿元，每年增长4%.(1)求营业额前20季度的和.(2)请问哪年哪季度营业额是利润的18%？

已知x1,x2∈R，若对任意的x2-x1∈S,f(x2 )-f(x1)∈S，则有定义：f(x)是S关联的.(1)判断和证明f(x)=2x-1是否在[0,+∞)关联？是否有[0,1]关联?(2)若f(x)是在{3}关联的，在x∈[0,3)时f(x)=x2-2x，求解不等式：2≤f(x)≤3.(3)证明：f(x)是{1}关联的，且是在[0,+∞)关联的，当且仅当“f(x)在[1,2]是关联的”.

已知a∈R，函数f(x)=，若f[f(√6)]=3，则a=__________.

(2lg2+lg3)/(2+lg0.36+2/3 lg8)

河北省对数函数

将函数f(x)=ex展开为x的幂级数，并求出收敛区间.( e=2.718为自然对数)

化简下式：(1 - c2)-1/2 - {[(1+c)(1-c)]1/2+c2[(1+c)(1-c)]-1/2}.

求(lg3+lg2)/(1/4 lg16++1/2 lg0.09)的值.(其中lg表示以10为底的对数)