高中数学-高考试题(中央政治学校 1941年解方程)

计算题（1941年中央政治学校）

解方程式

答案解析

暂无答案

讨论

高中数学

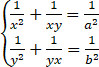
求证下列恒等式tan-1⁡m+tan-1⁡n=tan-1⁡(m+n)/(1-mn)

求证 sin⁡(x+y)/sin⁡(x-y)=(tanx+tany)/(tanx-tany)

△ABC 之边 AC 之三等分点之中，设近于 A 之点为 D，而 BC 之中点为 E时，则 AE 为 BD 所二等分.

若三角形的两边不等，它的对不等边的两角也必不等，并且大角必对大边.

求证 1³+2³+3³+⋯+n³=[n(n+1)/2]²

解方程式3/x+6/(x-1)=(x+13)/(x(x-1))

某学生带银去买书籍等物; 要用所有银的1/4买字典，1/5买地理，1/6买文具，这样算，付价之后，还可以剩银23/10元; 问他带去银是多少?

某校招考学生，投考的有 540 人，考取 15%，是多少人?

设P点在椭圆所引之二切线与其长轴之夹角为θ1,θ2，试就下列情形分别求P之轨迹.(1).tanθ1+tanθ2 为一定值.(2).cotθ1+cotθ2 为一定值.

试证=(sin⁡(c-a)sin⁡(a-b))/sin⁡(b+c) · [-2 sin⁡(b+c) sin⁡(b-c) ]=-2sin⁡(b-c)sin⁡(c-a)sin⁡(a-b)

解方程

设二次函数f(x)=ax2+bx+c(a>0)，方程f(x) - x=0的两个根x1,x2满足0<x1<x2<1/a.(Ⅰ)当x∈(0,x1 )时，证明x<f(x)<x1；(Ⅱ)设函数f(x)的图像关于直线x=x0对称，证明x0<x1/2.

根据指令(r,θ)(r≥0,-180°<θ≤180°),机器人在平面上能完成下列动作:先原地旋转角度θ(θ为正时,按逆时针方向旋转θ;θ为负时,按顺时针方向旋转-θ),再朝其面对的方向沿直线行走距离r.(I)现机器人在直角坐标系的坐标原点,且面对x轴正方向.试给机器人下一个指令,使其移动到点(4,4).(Ⅱ)机器人在完成该指令后,发现在点(17,0)处有小球正向坐标原点做匀速直线滚动.已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位).

设a∈R，函数f(x)=，若f(x)在区间(0,+∞)内恰好有6个零点，则a的取值范围是【】

红旗大队粮食产量逐年增加，1973年产量为90万斤，连续三年平均每年比前一年增产10%，这个大队从1973年到1976年总共生产粮食多少万斤？(精确到0.1)

已知2lgx+lg2=lg⁡(x+6)，求x.

求等式=125中x的值.

解方程：1/(x-1)+1=(4x-2)/(x2 - 1).

解方程lg(x-5)+lg(x+3)-2lg2=lg(2x-9).

解方程组并讨论a取哪些实数时，方程组(1)有不同的两实数解；(2)有相同的两实数解；(3)没有实数解.

方程(x2006+1)(1+x2+x4+⋯+x2004 )=2006x2005的实数解的个数为__________.

函数

某工厂今年七月份的产值为100万元，以后每月产值比上月增加20%，问今年七月份到十月份总产值是多少？

某工厂第三年产量比第一年增长21%,问平均每年比上一年增长百分之几?又第一年的产量是第三年的产量的百分之几?(精确到1%)

函数y=(3x-3-x) cos⁡x在区间[-π/2,π/2]的图像大致为【】

已知函数f(x),g(x)的定义域均为R，且f(x)+g(2-x)=5,g(x)-f(x-4)=7．若y=g(x)的图像关于直线x=2对称，g(2)=4，则f(k)【】

如图是下列四个函数中的某个函数在区间[-3,3]的大致图像，则该函数是【】

在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献．如图描述了一定条件下二氧化碳所处的状态与T和lg⁡P的关系，其中T表示温度，单位是K；P表示压强，单位是．下列结论中正确的是【】

函数f(x)=1/x+的定义域是_________．

设函数f(x)=若f(x)存在最小值，则a的一个取值为________；a的最大值为___________．

已知函数f(x)=，则f(f(1/2))=________；若当x∈[a,b]时，1≤f(x)≤3，则b-a的最大值是_________．

已知函数f(x)的定义域为[0,+∞)，且满足f(x)=f(1/(1+x))，记函数的值域为Af，若a>0，满足{y│y=f(x),x∈[0,a] }=Af，则实数a的取值范围为__________.