函数y=(3x-3-x) cosx在区间[-π/2,π/2]的图像大致为【 】
A、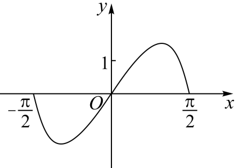
B、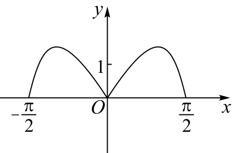
C、
D、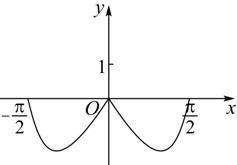
函数y=(3x-3-x) cosx在区间[-π/2,π/2]的图像大致为【 】
A、
B、
C、
D、
A令f(x)=(3x-3-x) cosx,x∈[-π/2,π/2],则f(-x)=(3-x-3x) cos(-x)=-(3x-3-x) cosx=-f(x),所以f(x)为奇函数,排除BD;又当...
查看完整答案如果下图是周期为2π的三角函数y=f(x)的图象,那 么f(x)可以写成【 】
函数y=tan(1/2 x - 1/3 π)在一个周期内的图像是【 】
已知函数 f(x) = sinx + 1/sinx, 则【 】
如图是函数 y = sin(ωx +φ) 的部分图像, 则 sin(ωx +φ) =【 】
函数 y = x cos x + sin x 在区间 [−π, π] 的图像大致为【 】
将函数y=3sin(2x+π/4)的图象向右平移 π/6 个单位长度, 则平移后的图像中与 y 轴最近的对称轴的方程是__________.
要得到函数y=sin(2x-π/3)的图像,只需将函数y=sin2x的图像(如图)【 】
函数y=arccos(cosx)(x∈[-π/2,π/2])的图像是【 】
如图是函数y=2sin(ωx+φ)(|φ|<π/2)的图像,那么【 】
设函数y=arctanx的图像沿x轴正方向平移两个单位所得到的图像为C.又设C'与C关于原点对称 ,那么C'所对应的图像是【 】
在同一平面直角坐标系内,分别画出两个方程y=-,x=-的图形,并写出它们交点的坐标.
在下列各图中,y=ax2+bx与y=ax+b (ab≠0)的图像只能是【 】
给定实数a,a≠0,a≠1,设函数y=(x-1)/(ax-1)(x∈R,x≠1/a).证明:(Ⅰ)经过这个函数图像上任意两个不同的点的直线不平行于x轴;(Ⅱ)这个函数的图像关于直线y=x成轴对称图形.
如图,图中曲线是幂函数y=xn在第一象限的图像.已知n取±2,±1/2四个值则相应于曲线C1,C2,C3,C4的n依次为【 】
设函数f(x) = 1 - (-1≤x≤0),则函数y=f-1(x)的图像是【 】