高中数学-高考试题(全国统考 1995年函数的图像)

单项选择（1995年全国统考）

函数y=-1/(x+1)的图像是【】

A、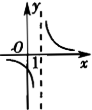

B、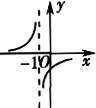

C、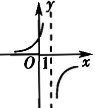

D、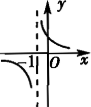

答案解析

B

讨论

高中数学

已知I为全集，集合M,N⊂I，若M∩N=N，则【】

设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的自然数n, an与2的等差中项等于Sn与2的等比中项.(I)写出数列{an}的前3项;(Ⅱ)求数列{an}的通项公式(写出推证过程);(Ⅲ)令bn=1/2(an+1/an +an/an+1 )(n∈N),求(b1+b2+⋯+bn-n).

如图，已知直线l过坐标原点，抛物线C的顶点在原点，焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上，求直线l和抛物线C的方程.

如图，已知A1B1C1-ABC是正三棱柱，D是AC的中点.(Ⅰ)证明AB1//平面DBC1;(Ⅱ)假设AB1⊥BC1，求以BC1为棱、DBC1与CBC1为面的二面角α的度数.

已知函数f(x)=tanx,x∈(0,π/2).若x1,x2∈(0,π/2),且x1≠x2,证明1/2 [f(x1)+f(x2)]>f((x1+x2)/2).

已知z=1+i.(Ⅰ)设ω=z2+3z ̅-4，求ω的三角形式；(Ⅱ)如果=1-i，求实数a,b的值.

在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到a1,a2,…,an,共n个数据,我们规定所测量物理量的“最佳近似值”a是这样一个量:与其他近似值比较,a与各数据的差的平方和最小.依此规定,从a1,a2,…,an推出的a=____________.

设圆锥底面圆周上两点A,B间的距离为2,圆锥顶点到直线AB的距离为,AB和圆锥的轴的距离为1,则该圆锥的体积为________.

已知sinθ + cosθ = 1/5,θ∈(0,π),则cotθ的值是________.

抛物线y2 = 8 - 4x的准线方程是________,圆心在该抛物线的顶点且与其准线相切的圆的方程是____________.

函数的图像

给定实数a,a≠0,a≠1，设函数y=(x-1)/(ax-1)(x∈R,x≠1/a).证明：(Ⅰ)经过这个函数图像上任意两个不同的点的直线不平行于x轴；(Ⅱ)这个函数的图像关于直线y=x成轴对称图形.

如图是下列四个函数中的某个函数在区间[-3,3]的大致图像，则该函数是【】

在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献．如图描述了一定条件下二氧化碳所处的状态与T和lg⁡P的关系，其中T表示温度，单位是K；P表示压强，单位是．下列结论中正确的是【】

函数f(x)=|x2-1|/x的图像为【】

Draw the graph of the equation (1) y = x³ - x² - x + 1.Use the graph to locate the roots of the equation (2) x³ - x² - x + 1 = 0.Check by solving the equation algebraically.

讨论方程式y=(x²+2x+3)/(2x²+3x+4)并绘其轨迹.

Determine the graph of y = x² + x + 1. Find the coordinates of its vertex and the equation of its axis.

讨论y=1/x² 所表示的轨迹，并作其图.

试判别方程x²+2xy-8y²+2x+14y-3=0之图形的性质.

试讨论方程y=x(x²-1)之图形：i) 对于原点、x轴、y轴对称否.ii) 与x轴之交点如何? 并作图.

函数

鸡蛋每个 80 元，鹅蛋每个 90 元，鸭蛋每个 70 元，用 9700 元买三种蛋共 120个，求各种蛋的个数.

解下列联立方程式x² - 4y² +x + 3y = 2x -y = 1

若x1,x2为方程式2x2-5x+3=0之二根，试求以x1/x2 与x2/x1 为根之方程式.

若a,b,c为方程式x³+px²+qx+r=0之根，试求以a-1/bc,b-1/ca,c-1/ab为根之方程式.

北京大学解方程

设a,b,c为方程式x³+px+q=0之三根，Sn=an+bn+cn.(1)展开下列行列式为p,q之函数∆=(2)表明∆>0时，a,b,c为三个不同实根；∆<0时，a,b,c三根中有一为实根，其余为二相配虚根；∆=0时，a,b,c为三实根且至少有二根相等.

解无理方程式+=，并就其结果讨论之.

设一三角形三边之长为方程式 x³ +px² + qx +r = 0 三根，式中 p,g,r 均为已知数，求此三角形之面积.

求方程式23x-31y=5,xy=13/32之解.

若方程式ax³+3bx²+3cx+d=0有二相等之根，则其系数间之关系为(bc-ad)²=4(ac-b²)(bd-c²)试证之.