设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的自然数n, an与2的等差中项等于Sn与2的等比中项.
(I)写出数列{an}的前3项;
(Ⅱ)求数列{an}的通项公式(写出推证过程);
(Ⅲ)令bn=1/2(an+1/an +an/an+1 )(n∈N),求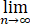 (b1+b2+⋯+bn-n).
(b1+b2+⋯+bn-n).
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的自然数n, an与2的等差中项等于Sn与2的等比中项.
(I)写出数列{an}的前3项;
(Ⅱ)求数列{an}的通项公式(写出推证过程);
(Ⅲ)令bn=1/2(an+1/an +an/an+1 )(n∈N),求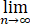 (b1+b2+⋯+bn-n).
(b1+b2+⋯+bn-n).
(I)由题意,当n=1时有(a1+2)/2=,S1=a1,∴(a1+2)/2=,解得a1=2.当n=2时有(a1+2)/2=,S1=a1+a1.将a1=2代入,整理得(a1-2)2=16.由a1>0,解得a1=6.当n=3时有(a3+2)/2=, S1=a1+a1+a3.将a1=2,a1=6代入,整理得(a3-2)2=64.由a3>0,解得a3=10.故该数列的前3项为2,6,10.(Ⅱ)由(I)猜想数列{an}的通项公式an=4n-2.由题意,有(an+2)/2=(n∈N),整理得Sn=1/8 (an+2)2,由此得Sn+1=1/8 (an+1+2)2,∴ an+1=Sn+1-Sn=1/8[(an+1+2)2-(an+2)2],整理得...
查看完整答案求极限[1/(n2+1)+2/(n2+1)+3/(n2+1)+⋯2n/(n2+1)].
已知等比数列{an}的公比q>1,并且a1=b(b≠0),求(a1+a2+a3+⋯+an)/(a6+a7+a8+⋯+an ).
已知{an}是等比数列,如果a1+a2+a3=18,a2+a3+a4=-9,且Sn=a1+a2+⋯+an,那么Sn 的值等于【 】
已知{an}是公差不为零的等差数列,如果Sn是{an}的前n项和,那么(nan)/Sn )等于______.
[n(1-1/3)(1-1/4)(1-1/5)…(1-1/(n+1))]的值等于【 】
已知等差数列前三项为a,4,3a前n项的和为Sn,Sk=2550.(Ⅰ)求a及k的值,(Ⅱ)求 (1/S1 +1/S2 +⋯+1/Sn ).